Wedges and Inclined Planes

Hi, and welcome to this review of wedges and inclined planes! In this video, we’ll take a closer look at these simple machines and discover how they’re used to reduce the amount of force needed to do work. Let’s get started!

In order to simplify our discussion of simple machines, it’s helpful to introduce the idea of mechanical advantage. Mechanical advantage as a formula is \(MA=\frac{\text{F}_{o}}{\text{F}_{i}}\). Essentially, this is a simple mathematical relationship that describes how we can reduce the amount of force needed to do work by increasing the distance over which a force is applied.

In physics, “work” has a technical definition. Work results when force is applied to an object and the object is displaced. The amount of work required to move an object a certain displacement always remains equal, regardless of mechanical advantage. So in human terms, lifting a box is harder than sliding it up a ramp, but the “work” accomplished in terms of physics is the same. In physics, mechanical advantage is what allows humans to accomplish more work using less force. Mechanical advantage is also involved in the reverse: when you want to use more force over a shorter distance. That may sound counterproductive, but there are many everyday situations where you want the output force to be less than the input force. For example, when you sweep with a broom, you use small movements with your hands to make bigger movements with the end of the broom. In short, a mechanical advantage greater than one increases the output force, and a mechanical advantage less than one increases the output distance.

This physics principle is called conservation of energy.

Let’s take a look at mechanical advantage using an inclined plane, which we typically call a ramp.

The Inclined Plane

Most likely, you’ve experienced a situation in which you want to lift an object that is too heavy to lift by yourself. For this example, imagine you’re loading your freshly packed belongings onto a moving truck, when you come across a large box that’s full of bulky textbooks. The box is heavier than you thought it would be, and you cannot lift it directly onto the truck. In other words, you cannot provide the force to lift it yourself. So, what do you do?

Well, regardless of how you get the box into the truck, the amount of work that’s needed will stay the same.

However, if you place a ramp between the surface you want to lift the box from and the place you want to move the box to, you can reduce the amount of force needed.

\(\text{Work}_{\text{lift}}=\text{Work}_{\text{ramp}}\)

If you lift it straight up, you have to lift with a force greater than the box’s weight to overcome the force of gravity. We can use the conservation of energy to find the force you must push it with over the distance along the ramp.

The work along the ramp is the force you push with times the distance along the ramp, and the work to lift the box straight up has to be greater than the weight times the height.

\(\text{Force}_{\text{ lift}}\cdot \text{Height}_{\text{ lift}}=\text{Force}_{\text{ ramp}}\cdot \text{Distance}_{\text{ ramp}}\)

We can actually rearrange the equation to get the forces on one side and the distances on the other side:

\(\frac{\text{Force}_{\text{ lift}}}{\text{Force}_{\text{ ramp}}}=\frac{\text{Distance}_{\text{ ramp}}}{\text{Height}_{\text{ lift}}}\)

Let’s say that the height of the truck bed is 1 meter and the length of the ramp is 4 meters. Plugging those numbers into the right side of the equation tells us that the mechanical advantage is 4 to 1.

\(MA=\frac{\text{Force}_{\text{ lift}}}{\text{Force}_{\text{ ramp}}}=\frac{\text{Distance}_{\text{ ramp}}}{\text{Height}_{\text{ lift}}}=41\)

If we solve this equation for the force we need to push the box up the ramp, we find that it is ¼ the force required to lift the box directly into the truck.

\(MA=\frac{\text{Force}_{\text{ lift}}}{\text{Force}_{\text{ ramp}}}=41\)
 
\(\text{Force}_{\text{ ramp}}=\frac{1}{4}\text{Force}_{\text{ lift}}\)

Hence, the inclined plane reduces the amount of force required to do the work.

If we estimate the mass of the box to be 50 kg and use 10 m/s² for the acceleration due to the force of gravity, we find the lift force is equal to 500 Newtons and the force required to push the box up the ramp is 125 Newtons, or, as noted, 1/4 the amount of the force required to lift the box directly onto the truck.

Yes, you do have to push for a longer distance to accomplish the same amount of work, but you were able to get your box onto the truck using less force.

Now, let’s discuss a simple machine that’s pretty similar to an inclined plane: the wedge.

The Wedge

A wedge is a simple machine that can be considered as two inclined planes combined.

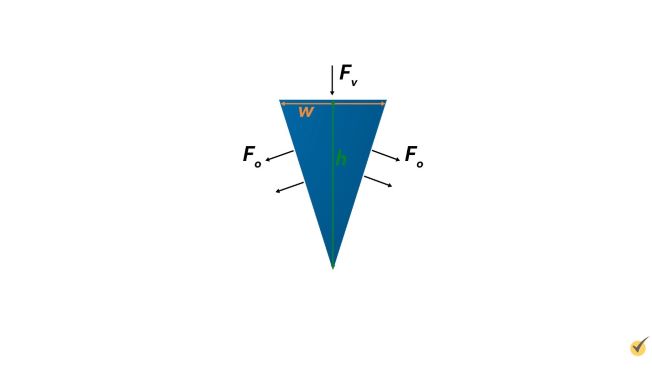
It provides mechanical advantage in much the same way a ramp does by distributing the force supplied to the top along the sides.

You apply a vertical force, \(\text{F}_{v}\), along the top width, \(W\), and that force gets distributed outward along the length of the wedge, labeled \(\text{F}_{o}\).

As you can see, the length along the sides is longer than the width along the top, which is where the force is provided.

Let’s take a look at how these dimensions and forces go into the mechanical advantage equation.

The mechanical advantage here can be simply stated as the height of the wedge divided by the width of the wedge, which can also be written as the outward force, \(\text{F}_{o}\), divided by the vertical force, \(\text{F}_{v}\).

Let’s take a look at a few real-life examples.

An ax used to split wood provides a striking force on a log, and that force is conducted outward along the sides of the ax to split the wood.

A chef’s knife is a wedge used to increase the force needed to cut through food effectively.

And an artist’s chisel is used to carve a sculpture by driving a wedge into the material with enough force to split it into the desired shape.