Hi, and welcome to this video on solving systems of equations with a linear and a quadratic equation!
In this video, we will take a look at two different ways to approach these problems: graphically and algebraically.
Let’s get started!
Linear Equations vs. Quadratic Equations
Before we get into how to solve these systems, let’s review the differences between linear and quadratic equations.
Linear equations are equations that graph as a line. They are equations that can be written as \(y=ax+b\). Notice that neither \(y\) nor \(x\) is to a power or a root.
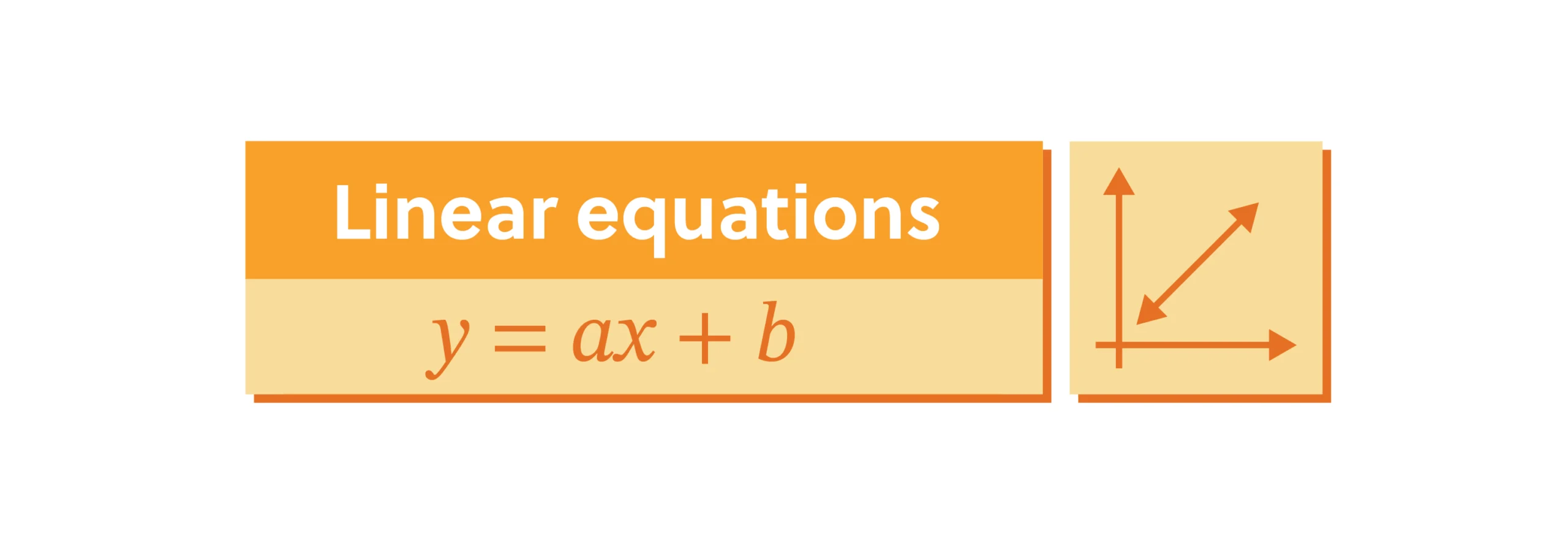
Quadratic equations are equations of the form \(y=ax^2+bx+c\), and they graph as a parabola. Notice that the \(y\)-term is still not to a power or a root, but we do have an \(x\)-term that is squared.
Solving Systems of Equations
When we solve systems of equations, we are taking two or more equations and finding the point, or points, where they intersect. When we have a linear equation and a quadratic equation, we will have zero, one, or two points of intersection.
Example #1
The first solving method we are going to look at is solving graphically. To do this, we simply graph our equations, either with a calculator or by hand, and see where the graphs intersect.
Let’s take a look at the equations:
If we graph these two equations next to each other, we get something that looks like this:
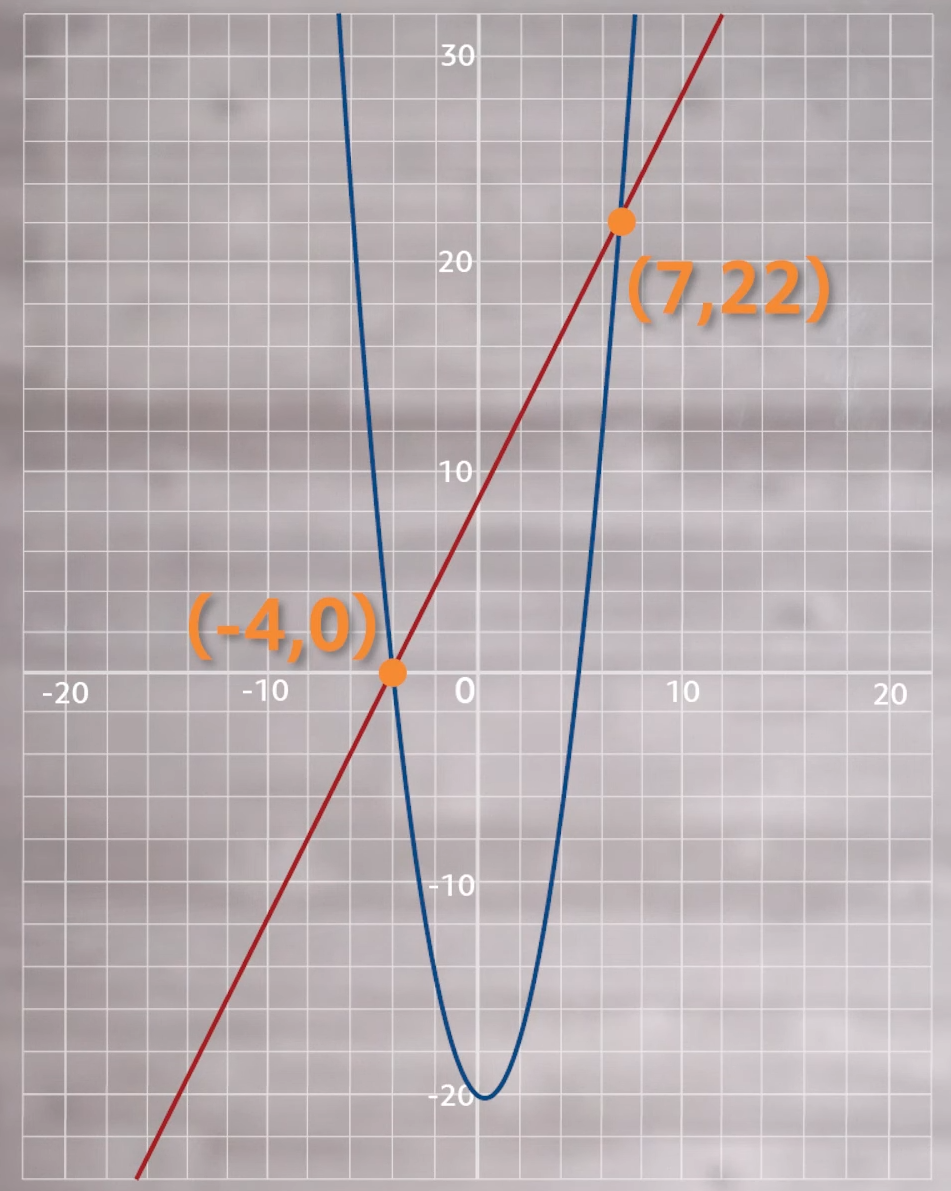
We can see from our graph that the two equations intersect at the points negative 4,0) and (7,22). (-4,0) and (7,22).
But what if we aren’t able to graph our equations? Well, that’s where algebra comes in. The other way to solve systems like this is very similar to the substitution method of solving regular systems of linear equations.
To find at what points our equations are equal to each other, we can substitute our \(y\)-values for each other. Looking back at our equations from earlier, we can see that since \(y=2x+8\), we can replace the \(y\) in \(y=x^2–x–20\) with \(2x+8\), or in other words, set our equations equal to one another.
When we write it out, that will look like this:
In order to solve a quadratic equation for \(x\), we need to get all of our terms on one side and zero on the other. To do this, we will subtract \(8\) and \(2x\) from both sides.
That gives us:
We can then factor this equation to get:
\(x=-4, 7\)
This tells us that our zeroes for this quadratic equation are -4 and 7. These are our values for \(x\) at the two points where our graphs intersect.
To find our \(y\)-values for each of these points, we simply want to plug in our \(x\)-values to either equation and solve for \(y\). I’m going to plug them into the linear equation because it will require fewer steps to get \(y\).
\(y=2(7)+8=14+8=22\)
So our points of intersection for this graph are \((-4,0)\) and \((7,22)\), which is what we found by graphing them.
If we wanted one more way to check our answers, we can plug them back into our original equations and make sure our answers match up.
Example #2
Let’s try one more example. Solve this system graphically and then algebraically:
\(y=2x^2–3x–28\)
In order to graph our linear equation, we want to first rearrange it so that y is by itself on one side. We can do this by adding y and subtracting 1 from both sides.
When we do this, it gives us:
Now we are able to graph both equations, and our graph will look like this:
We can see that our graphs intersect at the points \((-\frac{3}{2},-19)\) and \((9,107)\).
Now let’s check and see if we get the same answers using algebra.
If we use our rearranged linear equation, we are able to set our two equations equal to each other and solve.
We can subtract 12x and add 1 to both sides to get all of our terms on one side and zero on the other.
Now we want to factor our equation to get our x-values.
If we set each equation individually to equal zero, we get:
\(x–9=0\)
On this side, to solve for \(x\), we subtract 3 from both sides and then divide by 2. So \(x\) equals negative three-halves.
On this side, we just simply add 9 to both sides.
These are our \(x\)-values for our two points of intersection. Now we want to find our \(y\)-values.
So, we’re going to take our original equation, \(y= 12x – 1\), and plug in our \(x\)-value of negative three-halves. And then we’re gonna plug in our value of \(x =9\).
\(y=12(9)–1=108–1=107\)
Our two points of intersection are \((-\frac{3}{2},-19)\) and \((9,107)\). This is just like we found when graphing!
There’s one important thing to point out before we go. In both of these examples, our equations factored nicely to give us our \(x\)-values. This will not always be the case. Sometimes you will not be able to factor and will need to use the quadratic equation to find your \(x\)-values. After you find your \(x\)-values, follow the same steps to find your points of intersection.
I hope this video on solving systems with a linear and a quadratic function was helpful. Thanks for watching and happy studying!
System of Equation Practice Questions
The equations \(y=x^2+2x+3\) and \(2y-2x=10\) are graphed below. How many solutions are there for this system of equations?
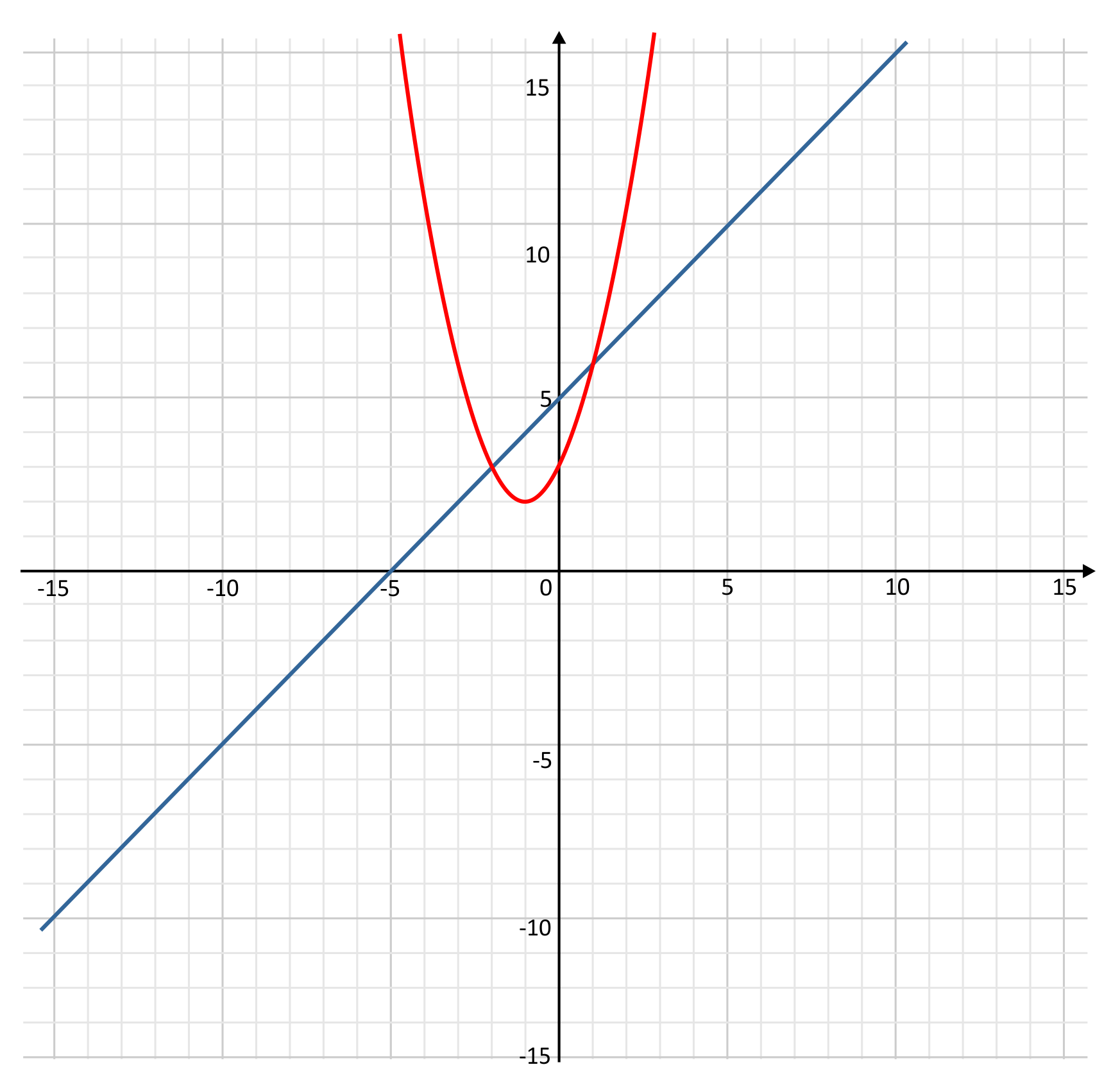
A linear equation and a quadratic equation will have either zero, one, or two points of intersection. Each point of intersection is a solution to the system of equations. In this case, we see that the graphs for these equations intersect exactly two times, at \((-2,3)\) and \((1,6)\). Therefore, there are two solutions, and B is the correct answer.
Which graph could be used to identify the solutions to the following system of equations?
\(y=x^2-5x+3\)
\(y=x-6\)
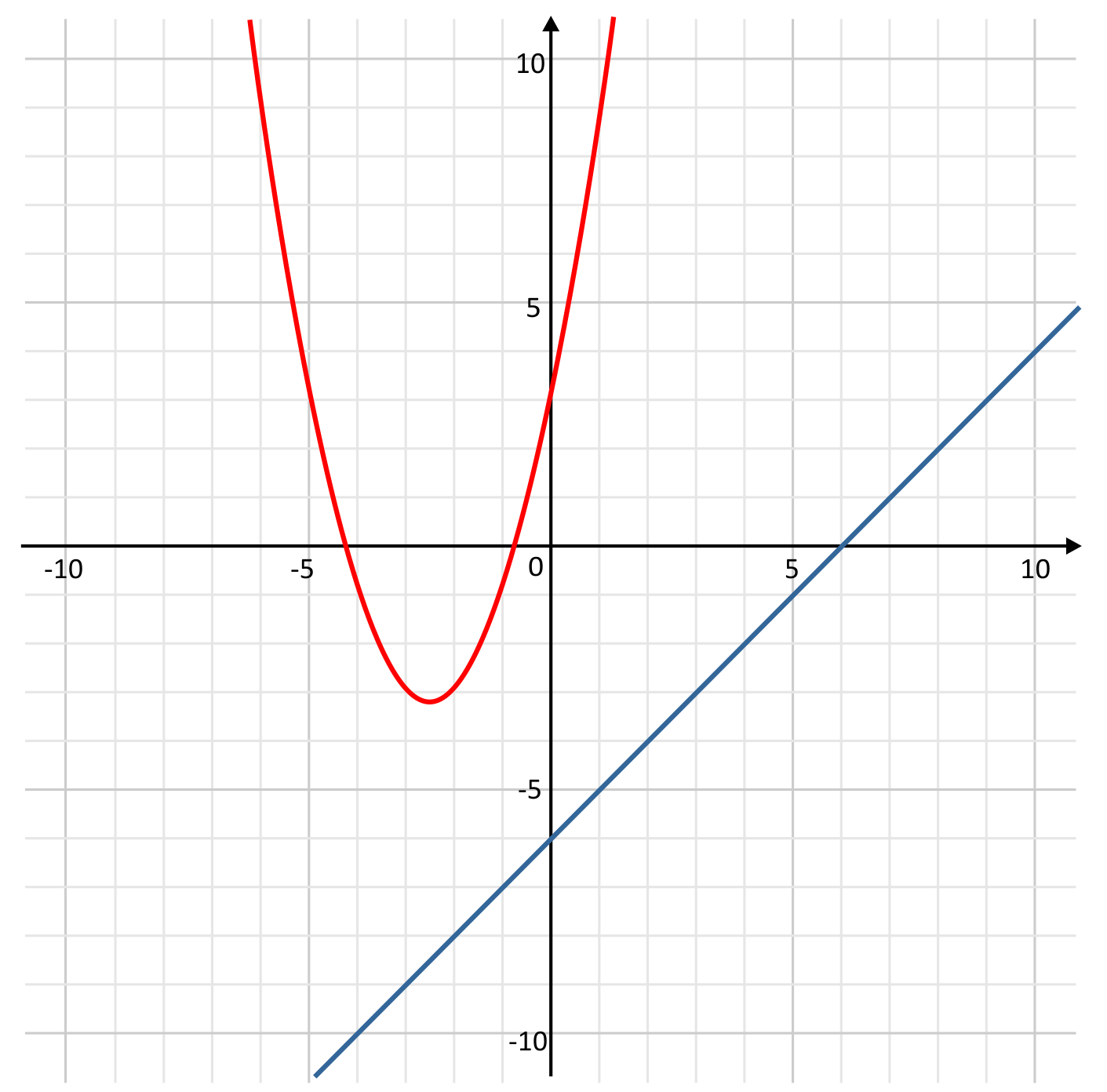
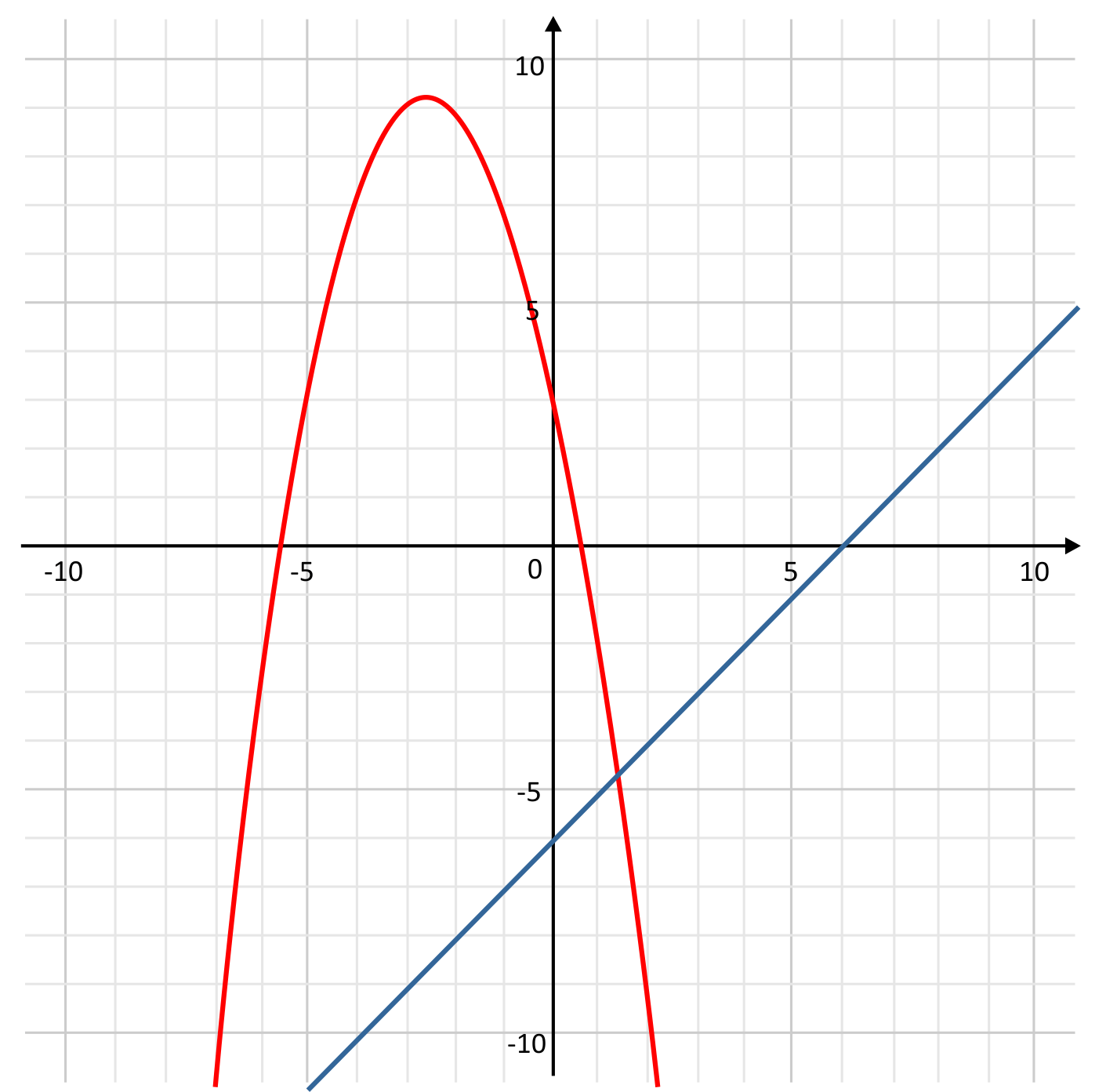
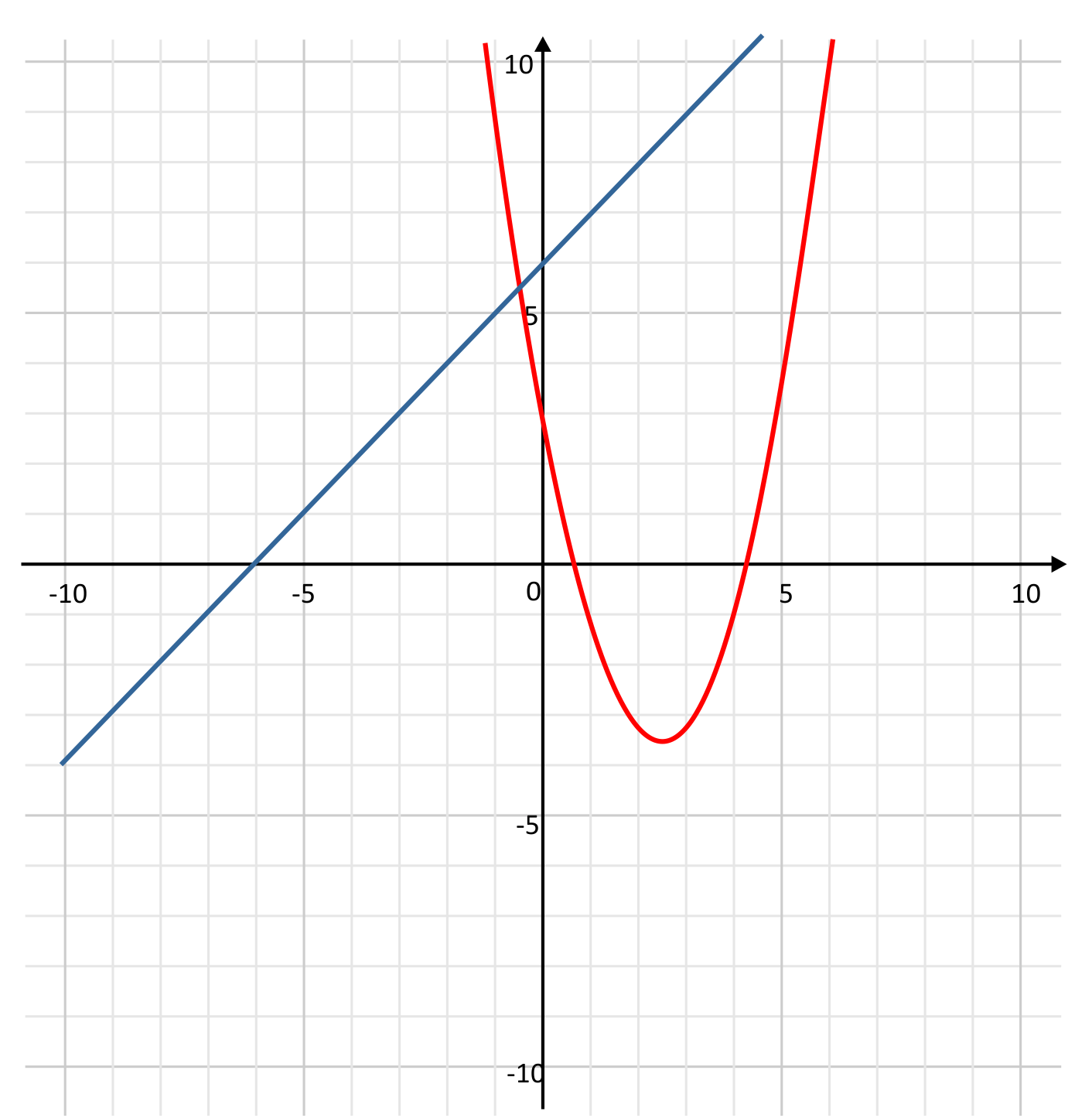
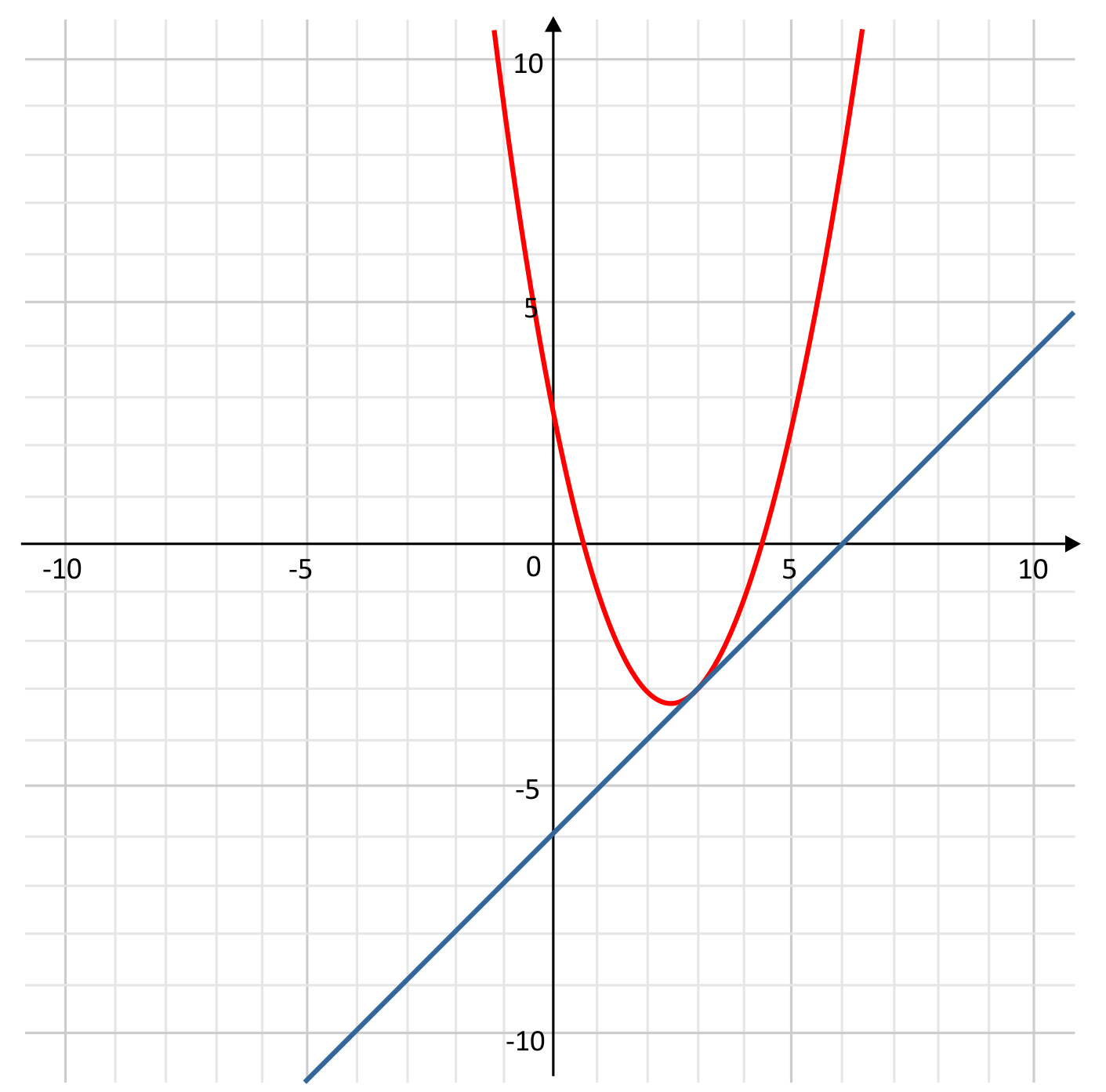
D is the correct answer because it correctly graphs both equations as stated. Answer A incorrectly graphed the quadratic function as \(y=x^2+5x+3\), shifting the parabola over \(5\) units. Answer B incorrectly graphed the quadratic function as \(y=-x^2-5x+3\), which flips the parabola in the opposite direction. Answer C incorrectly graphed the linear equation as \(y=x+6\), which changed the y-intercept from \(-6\) to \(6\). Therefore, D is the correct answer.
Two bus routes in Sunnydale can be graphed using the equations \(y=-x^2-3x+2\) and \(y=x+6\). Solve this system of equations algebraically to find out if there are any overlapping points on these two routes. If there are, what are the coordinate points of intersection for these two bus routes?
| \(-x^2-3x+2=x+6\) | To solve algebraically, set the two equations equal to one another. |
| \(-x^2-4x+2=6\) | To solve the equation for \(x\), move all terms to one side of the equation and set it equal to zero. To do so, move \(x+6\) to the left side of the equation. First, move \(x\) by subtracting \(x\) from both sides of the equation. Since \(x-x=0\), the \(x\)’s on the right side of the equation cancel out. Since \(-3x-x=-4x\), rewrite the equation using \(-4x\) on the left side of the equation. |
| \(-x^2-4x-4=0\) | Next, move the \(6\) on the right side of the equation to the left side of the equation. Subtract \(6\) from both sides of the equation. Since \(6-6=0\), write \(0\) on the right side of the equation. Since \(2-6=-4\), rewrite the equation using \(-4\) on the left side of the equation. |
| \(x^2+4x+4=0\) | From here, simplify the equation by multiplying each term by \(-1\). Doing so makes each term positive, and having positive terms makes the equation easier to work with. |
| \((x+2)(x+2)=0\) | Rewrite \(ax^2+bx+c=0\) in factored form, \((x+\text{_})(x+\text{_})=0\). To factor \(x^2+4x+4=0\), identify two numbers with a product of \(c\), which is \(4\), and a sum of \(b\), which is also \(4\). These two numbers are \(2\) and \(2\). \(2+2=4\) and \(22=4\). |
| \(x+2=0\) \(x+2-2=0-2\) \(x=-2\) | Next, separate \((x+2)(x+2)=0\) into two separate equations and solve for \(x\). Since both equations are identical, \(x=-2\) for both. This indicates that there is one solution to the system of equations. |
| \(y=-x^2-3x+2\) \(y=-(-2)^2-3(-2)+2\) \(y=-4+6+2\) \(y=4\) \(y=x+6\) | To identify the \(y\)-value for this point, substitute \(-2\) for \(x\) back into the original equations, \(y=-x^2-3x+2\) and \(y=x+6\). Since \(x=-2\) and \(y=4\), the point of intersection is \((-2,4)\). |
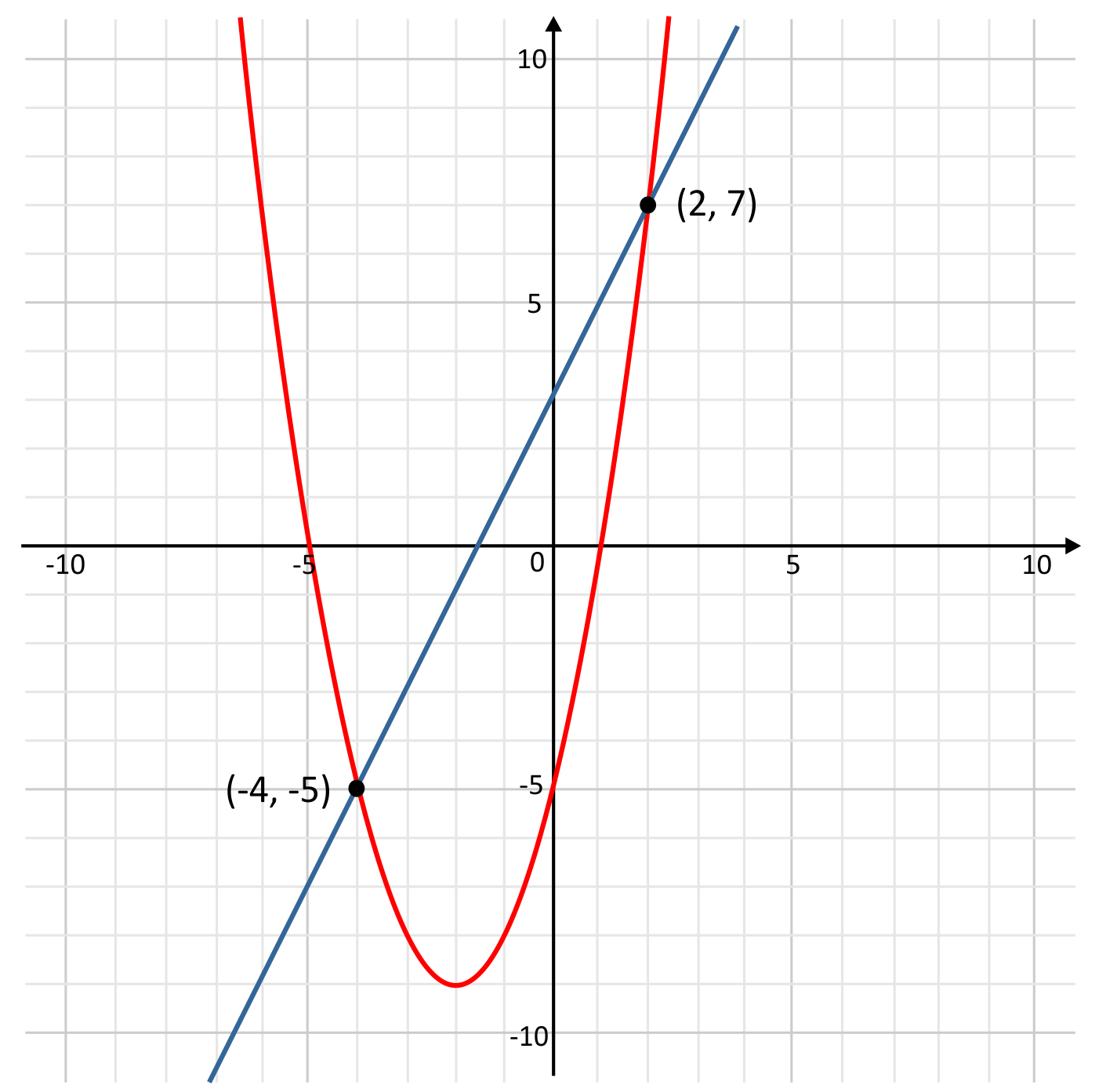
Which ordered pair is a possible solution to the system of equations shown below? Use a graph to help you solve.
\(y=x^2+4x-5\)
\(y=2x+3\)
When graphed, the two equations intersect at two points, \((-4,-5)\) and \((2,7)\). There are two solutions to this system of equations. Therefore, \((-4,-5)\) is one possible solution and C is the correct answer.
Stephanie is a city planner who is analyzing a map of street intersections to see where stoplights need to be installed. Specifically, she is looking at two streets that can be graphed using the equations \(x+y=5\) and \(y+1=3x^2+2x\). Solve this system of equations algebraically to find the coordinates for points of intersection on these two streets.
| \(x+y=5\) \(x-x+y=5-x\) \(y=-x+5\) \(y+1=3x^2+2x\) | Start by rewriting both equations in standard form, \(y=mx+b\) for the linear equation and \(y=ax^2+bx+c\) for the quadratic equation. In standard form, the two equations are \(y=-x+5\) and \(y=3x^2+2x-1\). |
| \(-x+5=3x^2+2x-1\) | To solve algebraically, set the two equations equal to one another. |
| \(5=3x^2+3x-1\) | To solve the equation for \(x\), move all terms to one side of the equation and set it equal to zero. To do so, move \(-x+5\) to the right side of the equation. First, move \(x\) by adding \(x\) to both sides of the equation. Since \(-x+x=0\), the \(x\)’s on the left side of the equation cancel out. Since \(2x+x=3x\), rewrite the equation using \(3x\) on the right side of the equation. |
| \(0=3x^2+3x-6\) | Next, move the \(5\) on the left side of the equation to the right side of the equation. Subtract \(5\) from both sides of the equation. Since \(5-5=0\), write \(0\) on the left side of the equation. Since \(-1-5=-6\), rewrite the equation using \(-6\) on the right side of the equation. |
| \(3x^2+3x-6=0\) | Write the equation in standard form by flipping both sides of the equation and rewriting it as \(3x^2+3x-6=0\). |
| \((3x-3)(x+2)=0\) | Rewrite \(ax^2+bx+c=0\) in factored form, \((x+\text{_})(x+\text{_})=0\). To factor \(3x^2+3x-6=0\), identify two numbers with a product of \(c\), which is \(-6\), and a sum of \(b\), which is \(3\). Since \(a=3\), the factored equation looks like \((3x+\text{_})(x+\text{_})=0\). \(-3\) and \(2\) are the two numbers that work for the factored equation. \(-3\times2=-6\) and \(-3x+2(3x)=3x\). |
| \(3x-3=0\) \(3x-3+3=0+3\) \(3x=3\) \(\frac{3x}{3}=\frac{3}{3}\) \(x=1\) | Next, separate \((3x-3)(x+2)=0\) into two separate equations and solve for \(x\). Start with \(3x-3=0\). Isolate the variable to find that \(x=1\). |
| \(x+2=0\) \(x+2-2=0-2\) \(x=-2\) | Solve \(x+2=0\). Isolate the variable to find that \(x=-2\). |
| \(x+y=5\) \((1)+y=5\) \(1-1+y=5-1\) \(y=4\) \(x+y=5\) | To identify the \(y\)-value for each point, substitute each \(x\)-value back into the original equation, \(x+y=5\), and solve. When \(x=1,y=4\). When \(x=-2,y=7\). Therefore, the two points of intersections are \((1,4)\) and \((-2,7)\). Therefore, B is the correct answer. |
