
Hi, and welcome to this review of sine! Today we’re going to dig into what sine functions are all about and take a look at three types of problems where you’ll find them.
Solving Right Triangles
First, let’s look at the main use of trigonometric functions, which is to solve right triangles.
Here’s an example:
Our goal is to find the measure of angle \(x\). We know all the side lengths, and know there is a right angle which measures 90 degrees. But the other two angles are unknown.
Because the sum of the interior angles of a triangle must add up to 180 degrees, we know that angle \(x\) and the other unknown angle must add up to 90 but we have no idea how they do so. They could both be 45 degrees or one could be 50 and the other 40 or 30 and 60 and so on.
There’s no way for us to know, unless we use a bit of trigonometry, specifically sine.
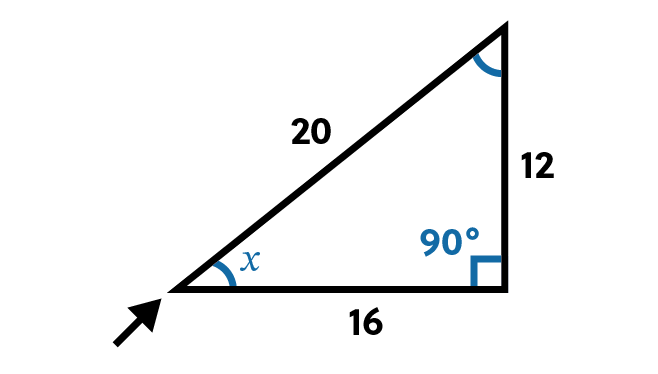
Sine, which is commonly abbreviated to S-I-N, is the ratio of the side opposite the angle we want to know over the hypotenuse of the right triangle.
\(\text{sin }θ=\frac{\text{opposite}}{\text{hypotenuse}}=\frac{\text{o}}{\text{h}}\)
Remember that the hypotenuse is the longest side and is always opposite the right angle, which is the largest angle in any right triangle.
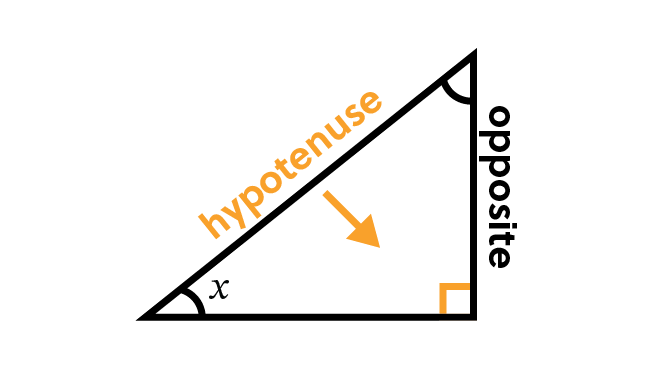
When dealing with trigonometric ratios, it’s common to use SOH-CAH-TOA to help you remember them. The first part of it, SOH, helps us remember that Sine is the Opposite over
the Hypotenuse.
Because the hypotenuse will always be longer than the opposite side, this means the possible values for sine when used in a triangle like this are between 0 and 1. In our sample triangle, the side opposite angle \(x\) has a length of 12 and the hypotenuse has a length of 20.
Now we know that the sine of x is equal to 0.6 when we convert the fraction to a decimal by dividing the numerator by the denominator.
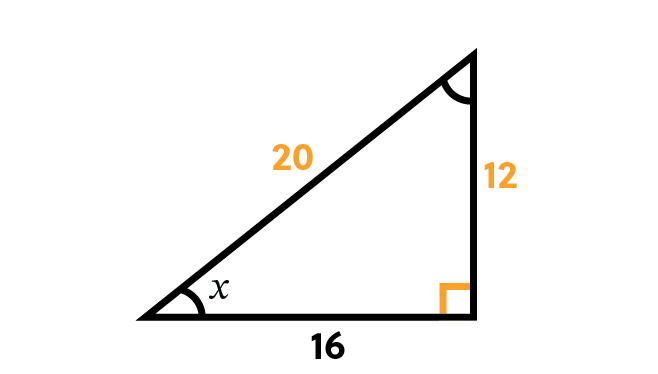
Now we need to use a calculator to find our angle. In the old days before calculators this had to be done by looking through pages and pages of SIN tables to find the value of SIN x that corresponded to the measure of angle x. That still works, but it’s easier on a calculator.
First, find the SIN button on your calculator. This button is usually used when you know the angle and you want to find the ratio of the opposite side to the hypotenuse. We want to do the opposite, and find the angle from the ratio that we have already calculated (0.6). So what we need is the ARC SIN, which is often labeled as ASIN or, even more commonly, as SIN-1. Note that the -1 exponent here does not represent the reciprocal, but the inverse operation of SIN. This is accessed by hitting the 2nd key and then the SIN key.
Okay, so we type in 0.6 and then 2nd and then SIN and our calculator displays 36.86989765,or approximately 36.87 degrees. We’ve done it!
Finding the Missing Side of a Triangle
We can also use sine to find a missing side if we happen to know an angle of the triangle and the hypotenuse. Here’s another sample problem:
Okay, let’s set up our equation. We know the angle is 30 degrees, so the left side of our equation is the sine of 30 degrees. This is set equal to the opposite side, which is \(x\), over the
hypotenuse, which is 14.
The sine of 30 degrees is a number that we can find by using our calculator. We just type in 30 and hit the SIN key and we get a value of 0.5. So now our equation looks like this:
To solve, we multiply both sides by 14 and we find that \(x\) has a value of 7. Success!
Okay, so far we have used sine to find a missing angle and a missing side in a right triangle. What else is it used for?
Graphing Using Sine
Our second use of sine is for graphing. Let’s set up the simplest sine function:
This is a sine wave. It’s maximum \(y\)-value is 1 and it’s minimum y-value is -1. That’s a bit different than in our triangle, where we couldn’t have a negative value of the sine function, but that was because our opposite and hypotenuse sides were always positive.
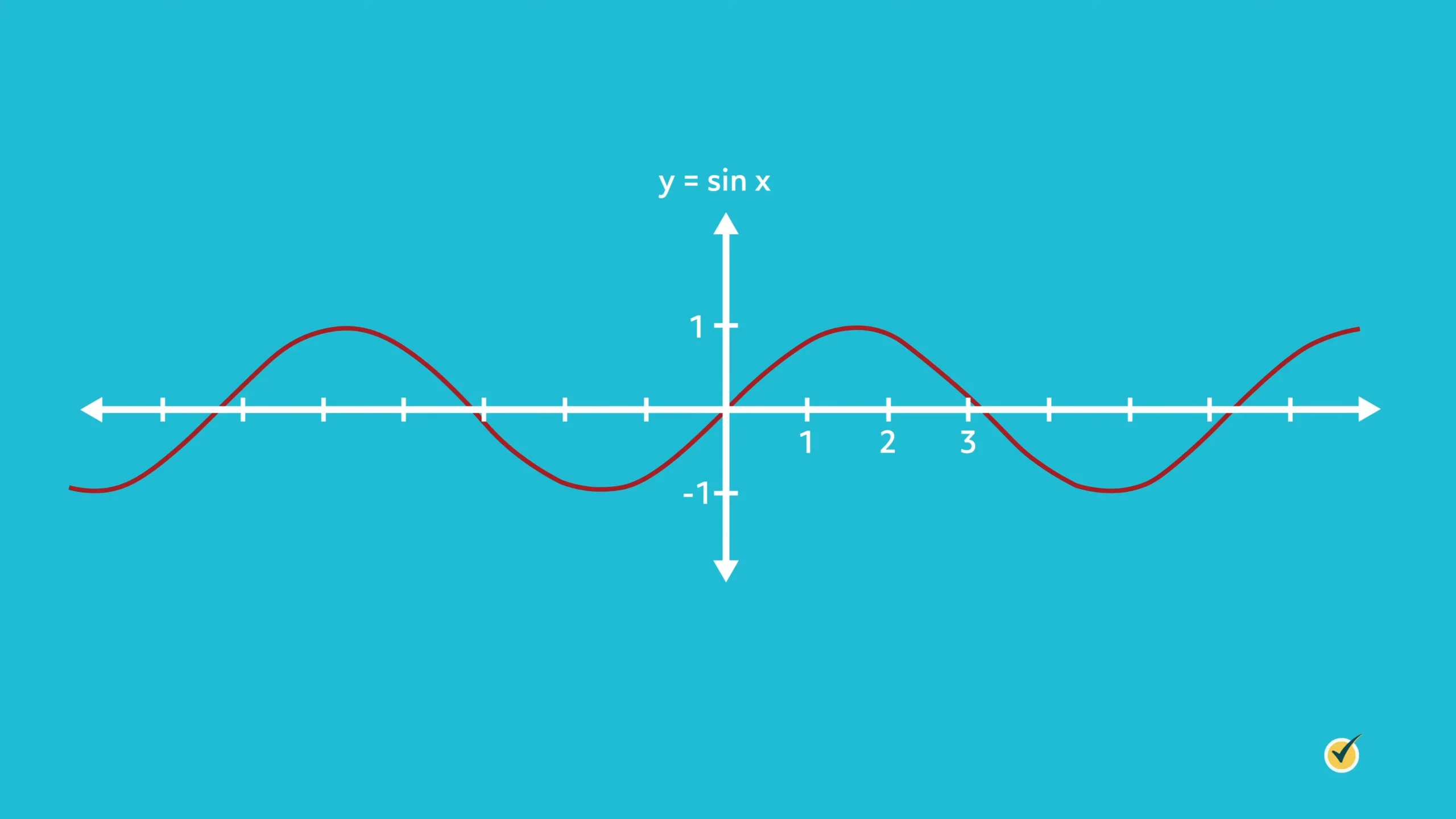
Let’s look closely at the \(x\)-values.
Notice that these are not angle measures, since there is no degree symbol on the numbers. Instead, we’re using radians. You may have noticed that on your calculator you can choose between degrees and radians. Converting between radians and degrees requires you to know that pi radians = 180 degrees.
Look at our graph. Since pi is approximately 3.14 we can look just to the right of the 3 on our \(x\)-axis and see that the graph touches the \(x\)-axis right where \(\pi\) is located. We can test this by making sure our calculator is in Radian mode (RAD), hitting the pi key and then the SIN key. We get a value of 0, which shows we interpreted that correctly.
Let’s try it again but this time in Degree mode (DEG). Let’s use the equivalent of pi which is 180 degrees. Make sure your calculator is in Degree mode, type in 180 and hit the SIN key. Again we get 0!
The peak of the wave is halfway between 0 and pi, so if we are in radian mode, hit the pi key and divide by two and then hit the SIN key we’ll get a value of 1.
Using Trig Identities
The third place we’ll see sine is when using trigonometric identities. There are a lot of trig identities, and they are used to simplify expressions or equations. It’s kind of like a puzzle where you need to find the right identity so that you can substitute and simplify by cancelling.
Let’s take a look at a relatively easy one:
We haven’t seen cosecant of \(x\) yet, but if we look it up we find that it is equal to the hypotenuse over the opposite, or, more usefully, the reciprocal of the sine!
Going back to our problem, we can substitute one over the sine of \(x\) for cosecant of \(x\), which give us this:
And that’s all there is to it! As you can see, sine comes in handy when graphing, solving problems with angles, and determining trigonometric identities.
I hope this review was helpful! Thanks for watching, and happy studying!
Sine Practice Questions
Solve for the measure of angle \(x\).
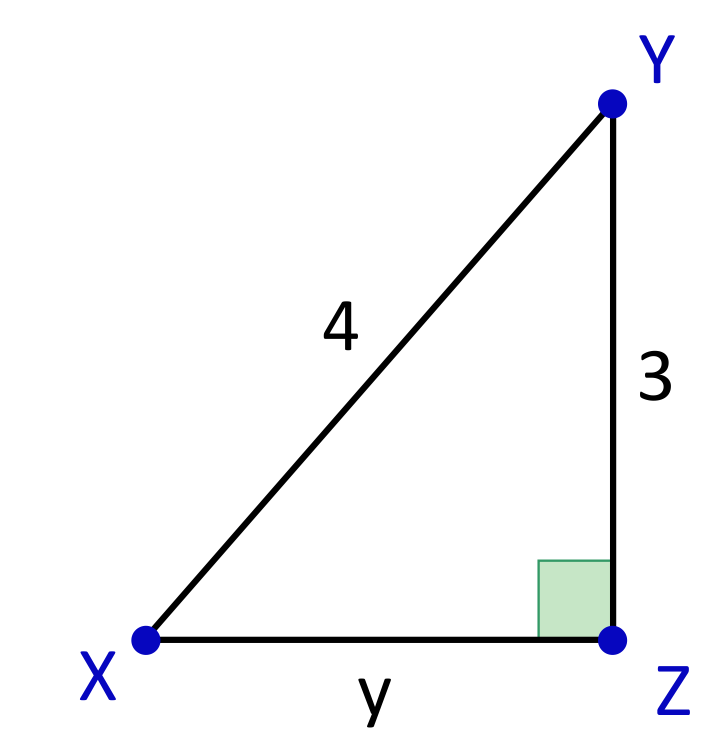
The opposite and hypotenuse side lengths are provided with the right triangle. This means that we can solve for angle \(x\) by using a sine trig function. The equation will start out as \(\text{sin}x=\frac{3}{4}\). In order to solve for \(x\), we need to use the inverse of the function, so the equation \(\text{sin}x=\frac{3}{4}\) becomes \(x=\text{sin}^{-1}(\frac{3}{4})\), which simplifies to approximately \(48.59°\).
Solve for the hypotenuse AB in the following right triangle.
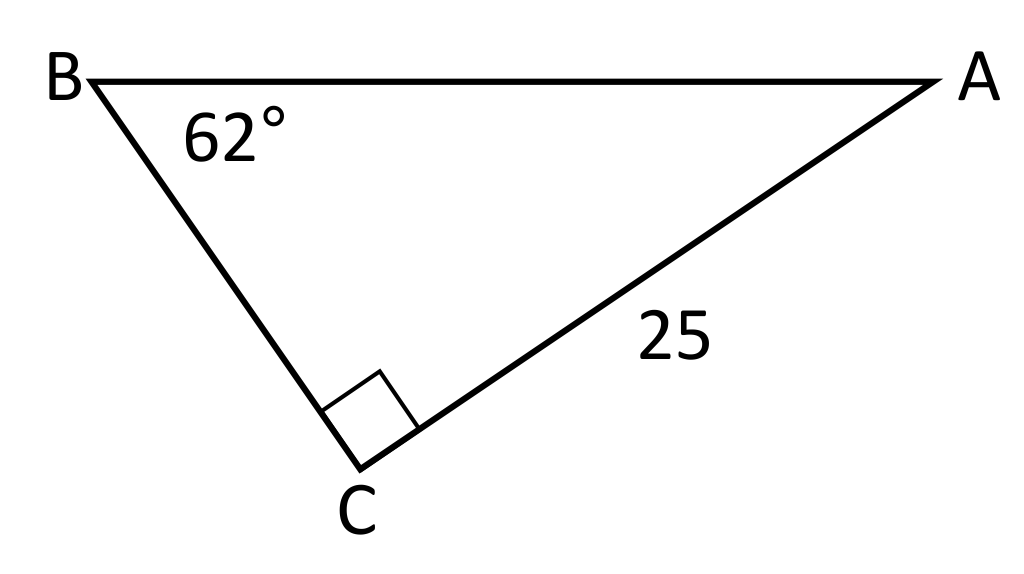
The sine trig function can be used to solve for the hypotenuse of this triangle by setting up the following equation: \(\text{sin}62=\frac{25}{x}\). \(\text{sin}62\) is equivalent to \(0.883\), so \(\text{sin}62=\frac{25}{x}\) becomes \(0.883=\frac{25}{x}\), which simplifies to approximately \(28.31\).
In order to solve for an unknown angle using the sine trig function, the ______ and ________ need to be provided.
SOH-CAH-TOA is a helpful mnemonic device to remember the three basic trig ratios: sine, cosine, and tangent. SOH refers to \(\text{sine}=\frac{\text{opposite}}{\text{hypotenuse}}\). When using the sine trig ratio, the opposite and hypotenuse need to be provided in order to solve for a missing angle measure.
Suppose you want to build a ramp that reaches a doorway that is \(4\) feet above the ground. How long will the ramp need to be if you want the angle of elevation to be \(20°\)?
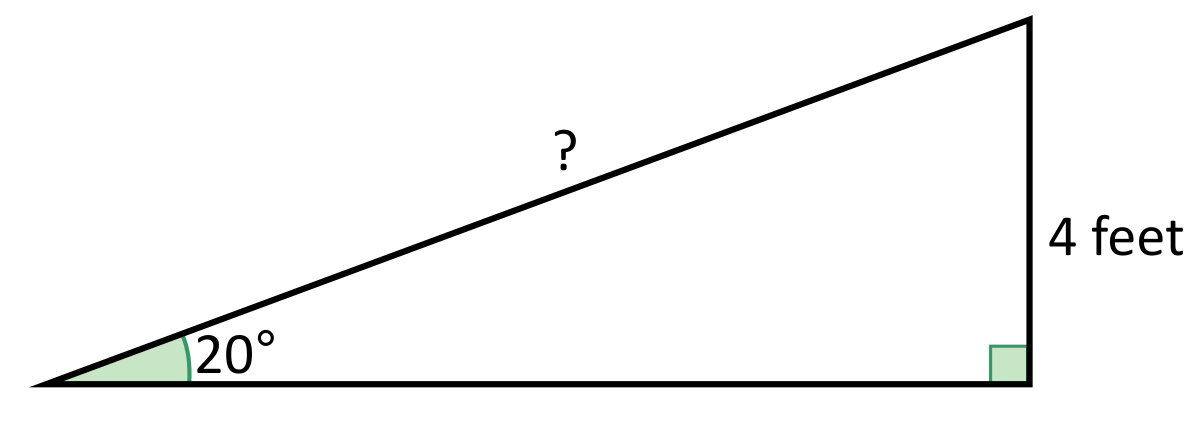
The sine trig function can be used to solve for the length of the hypotenuse using the equation \(\text{sin}20=\frac{4}{x}\). \(\text{sin}20\) is equivalent to \(0.3420\), so the equation \(\text{sin}20=\frac{4}{x}\) becomes \(0.3420=\frac{4}{x}\). This simplifies to approximately \(11.7\) feet.
How high off the ground is Jeremy’s kite if the string from the kite is extended to \(50\) meters, and the angle of elevation created from the ground and the kite is \(12°\)?
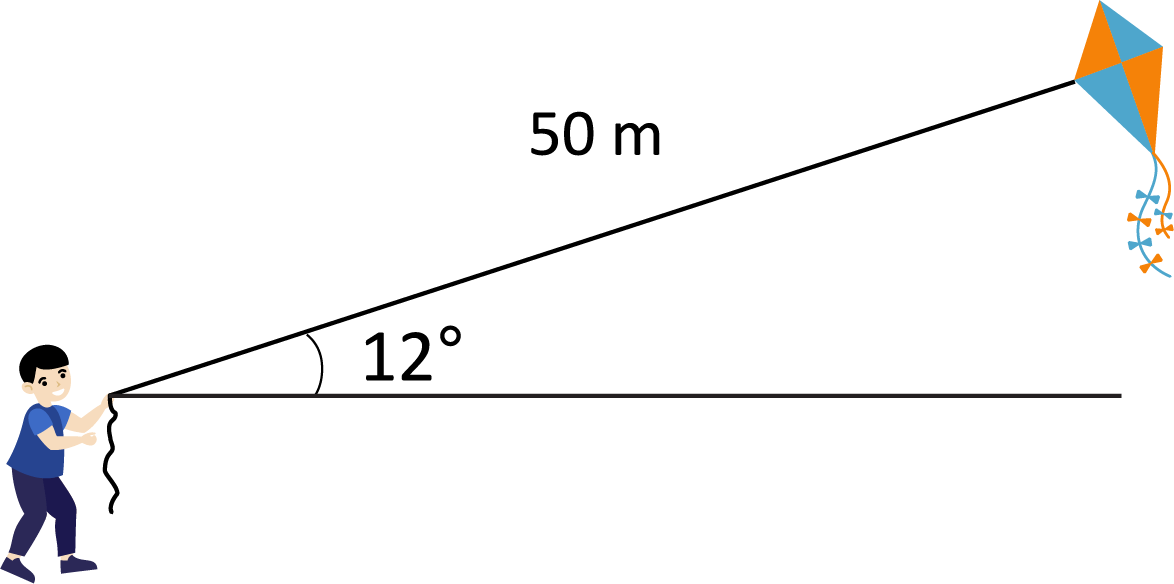
The height of the kite can be determined by setting up a trig function. The sine trig function will be used, and the equation will start as \(\text{sin}12=\frac{x}{50}\). \(\text{sin}12\) simplifies to \(0.2079\), so \(\text{sin}12=\frac{x}{50}\) becomes approximately \(0.2079=\frac{x}{50}\). When both sides of the equation are multiplied by \(50\), the value of \(x\approx10.4\) feet.