Reflecting Points on a Coordinate Plane
Hi, and welcome to this video about reflection! In this video, we will explore reflection of a figure over a line and reflection of a figure on a point. Let’s get started!
When we think of the term reflection, we most likely think of looking in a mirror or a still body of water. This idea is related to what happens when we reflect figures on the coordinate plane. Like I mentioned, there are two main types of reflections: reflections over a line and reflections on a point. Let’s start by looking at reflections over a line.
We can reflect a figure in the coordinate plane over any line in the coordinate plane. Here’s a triangle reflected over the line \(x=7\).
The triangle on the left is our original figure, or pre-image, named Triangle ABC. The triangle on the right is our reflected figure, or image, named Triangle A’B’C’. Prime notation designates the figure that is the image. Point A on the preimage corresponds to point A’ on the image, and so forth.
Now there are a few things to notice here:
Firstly, the preimage and image are congruent, but “flipped”.
You’ll also notice that all corresponding points on the preimage and image are the same distance from the line of reflection but in the opposite direction.
And lastly, the line of reflection bisects all segments connecting corresponding points of the preimage and image.
Now, here is a trapezoid being reflected over three different lines.
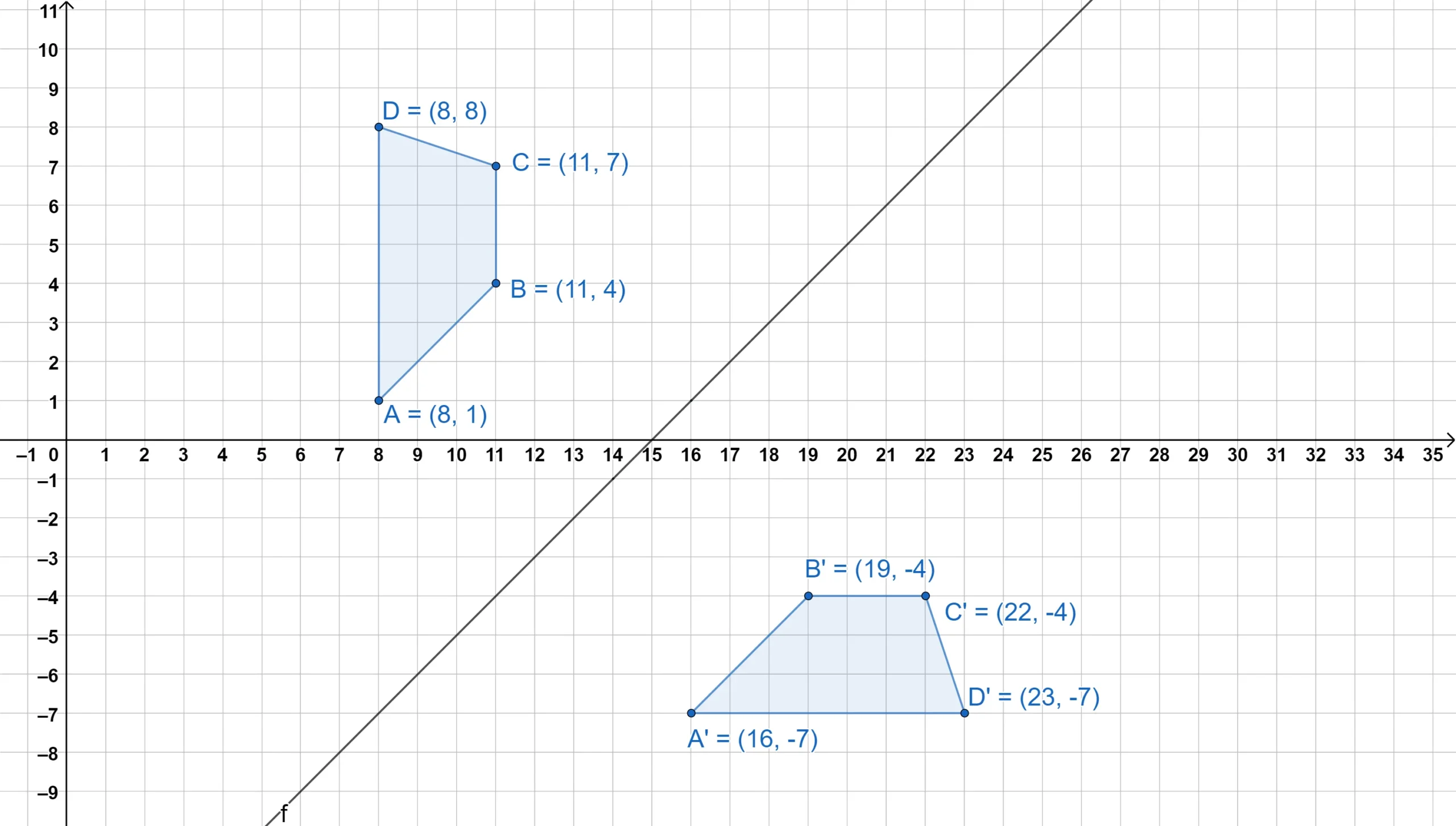
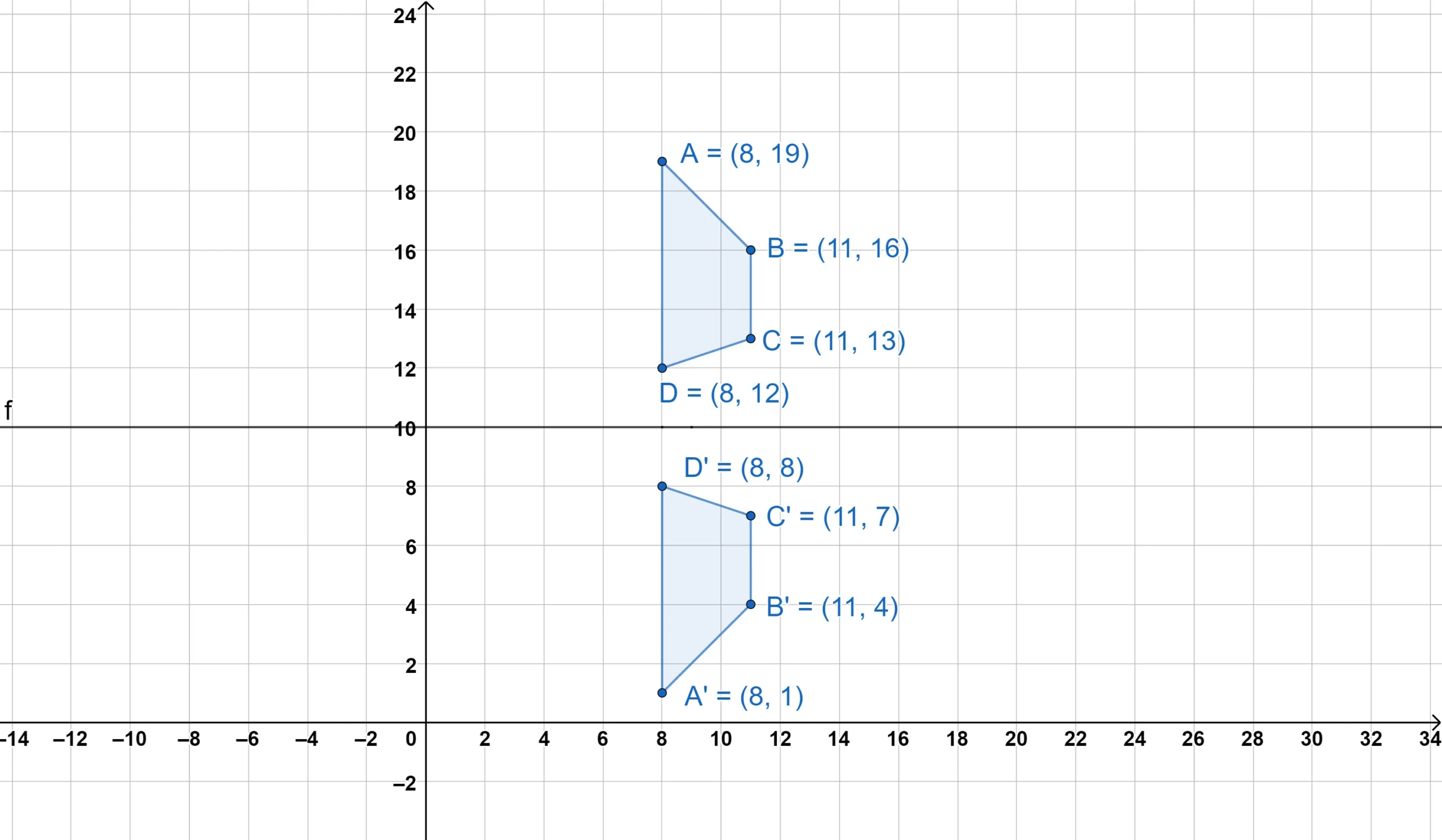
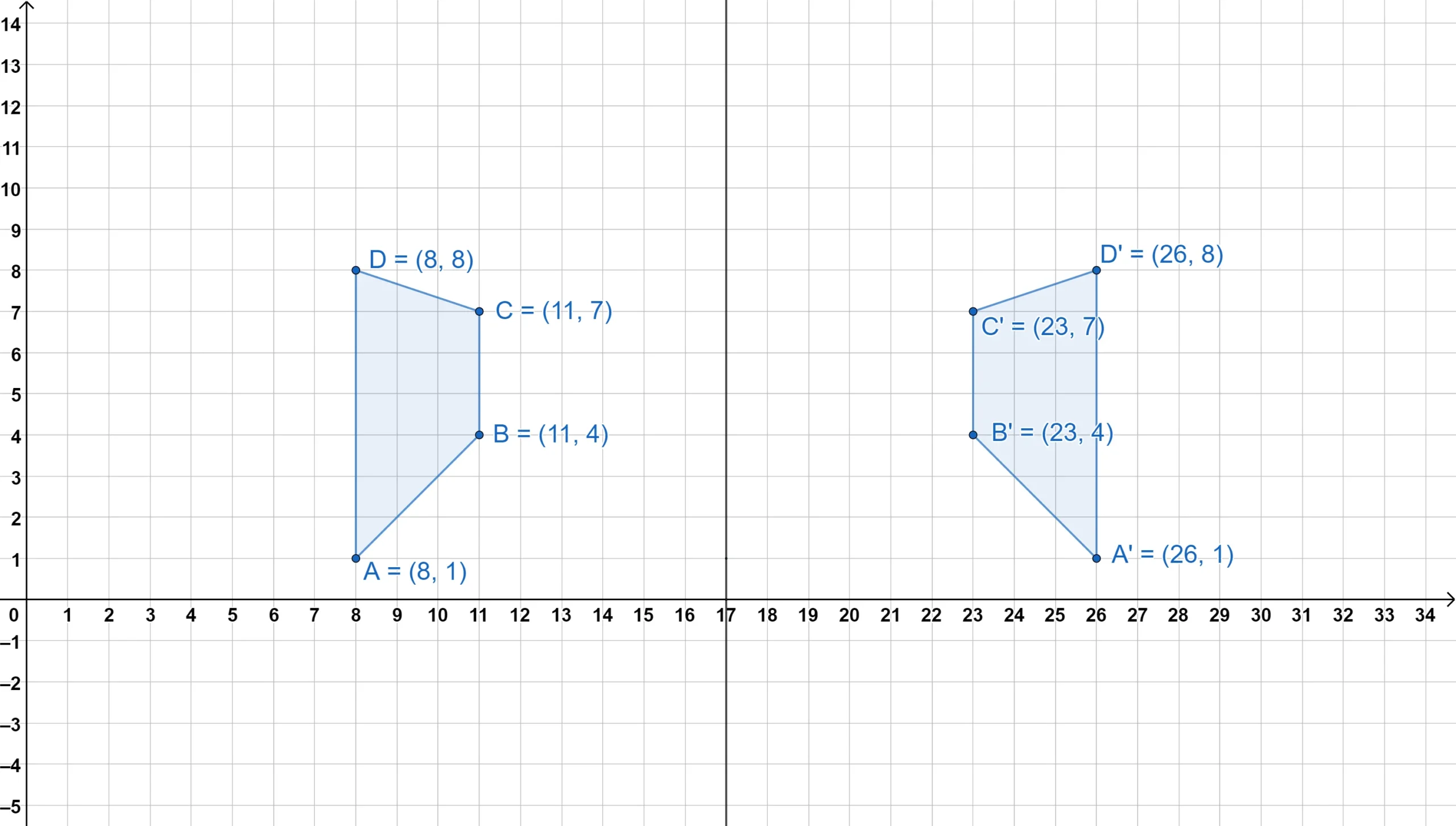
Notice how the three properties we just discussed hold true, but also notice how, to actually create a reflection, it often involves simply counting the distances between the line of reflection and the points, or adding and subtracting coordinates.
In some cases, the line of reflection may be on the edge – or even inside – the figure.
Three common ways to reflect figures are over the \(x\)-axis, \(y\)-axis, and the line \(y=x\). Something to notice as we look at these is that the signs of the coordinates change.
For example, when a figure is reflected over the \(x\)-axis, notice the \(y\)-coordinates change sign.
When a figure is reflected over the \(y\)-axis, notice the \(x\)-coordinates change sign.
When a figure is reflected over the line \(y=x\), notice that the coordinates change order.
We can also reflect a figure in the coordinate plane in any point on the coordinate plane. Here’s a dart reflected in the point (12,10).
The point the dart is reflected over is called, you guessed it, the point of reflection.
The properties of reflections in points are very similar to those of reflections over lines:
The preimage and image are congruent, but the image is a 180-degree rotation of the preimage.
All corresponding points on the preimage and image are the same, but opposite, distance from the point of reflection.
And, the point of reflection is the midpoint of all segments connecting corresponding points of the preimage and image.
Sounds just like reflection over a line, right?
Here is a kite being reflected over several different points.
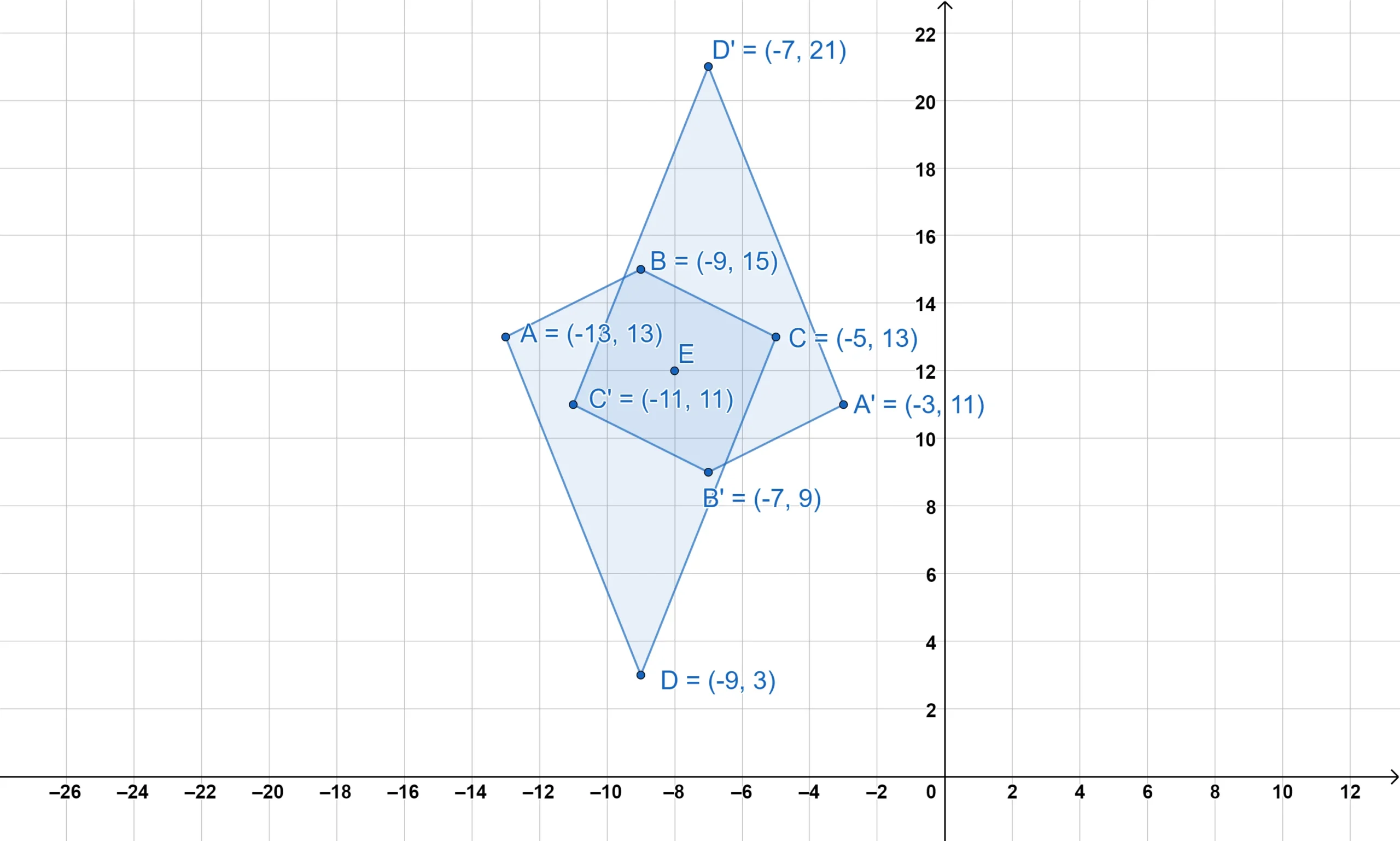
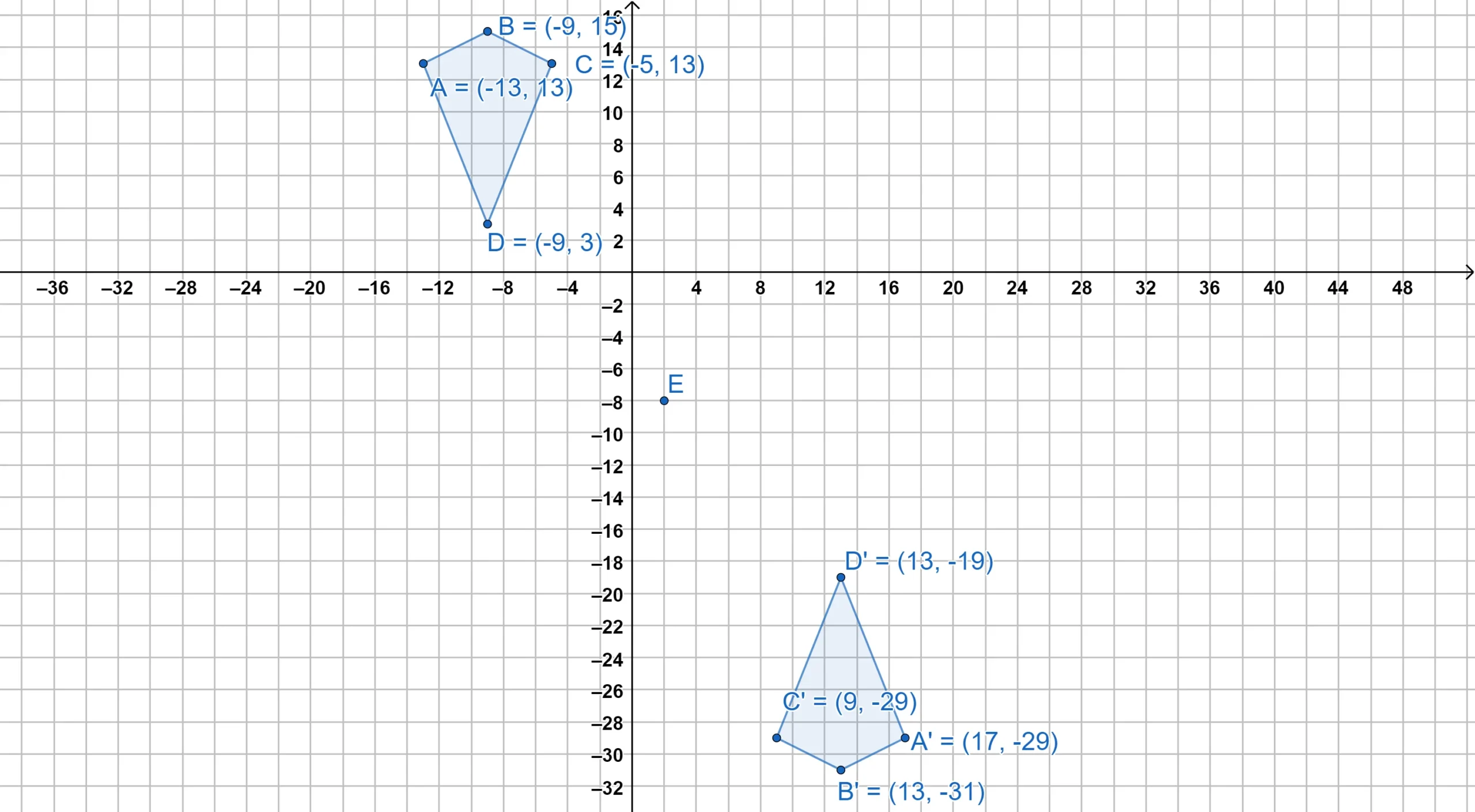
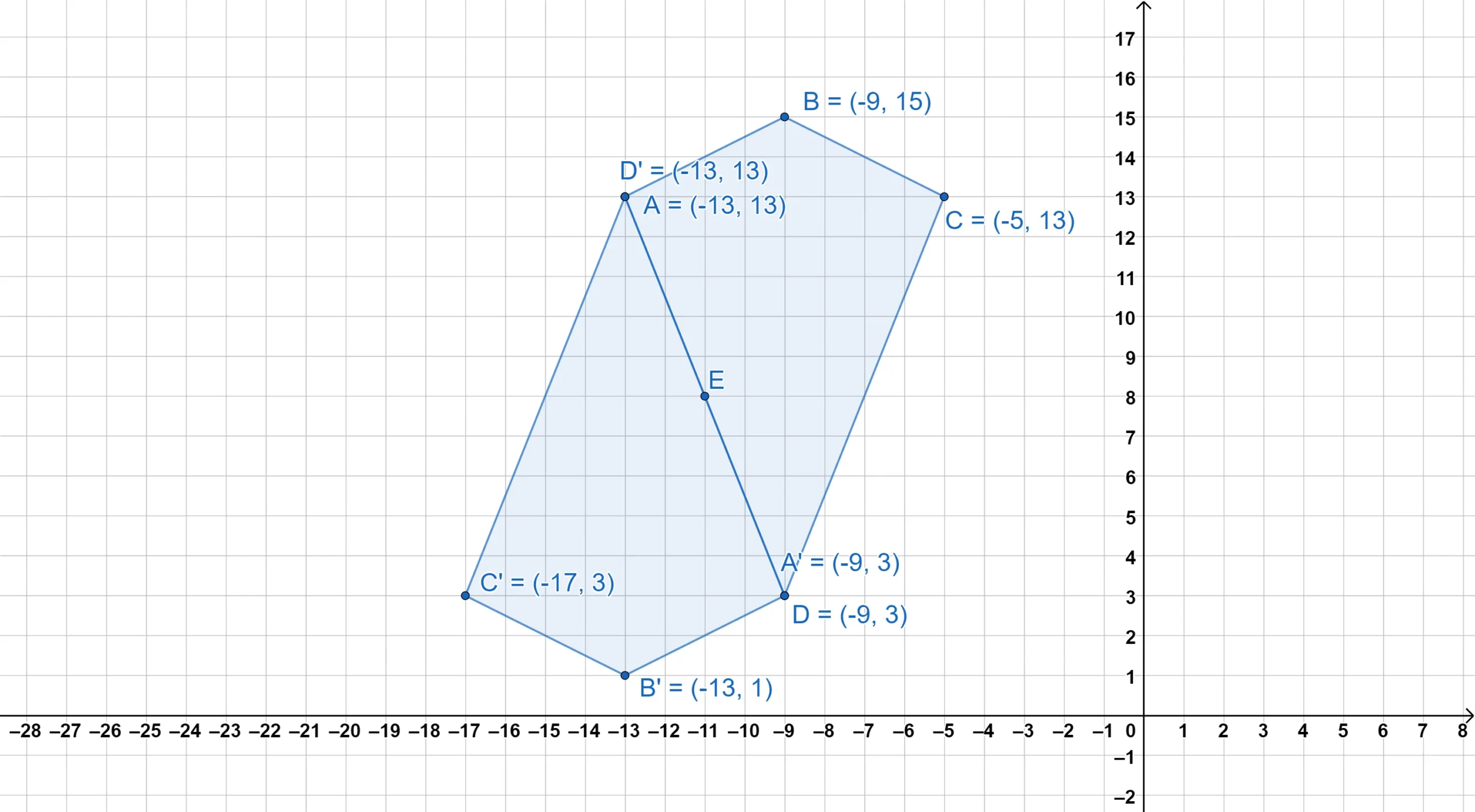
The point of reflection can be on the edge – or even inside – the figure. Notice how our properties still hold true.
And finally, let’s look at one last reflection. One often-used reflection is one about the origin (0,0). When a figure is reflected about the origin, the signs of all coordinates change.
That’s all for this video. Thanks for watching, and happy studying!
Reflecting Points on a Coordinate Plane Practice Questions
Triangle ABC, where A\((0,7)\), B\((3,-5)\), and C\((-3,5)\), is reflected across the \(x\)-axis to create triangle A’B’C’. What are the coordinates of Triangle A’B’C?
The rule for reflecting across the \(x\)-axis is \((x,y)\rightarrow (x,-y)\). When we apply this rule to the points of the vertices of Triangle ABC, we get A’\((0,-7)\), B’\((3,5)\), C’\((-3,-5)\).
Trapezoid PQRS, where P\((2,3)\), Q\((6,3)\), R\((8,1)\), and S\((0,1)\), is reflected across the line \(y=x\) to create Trapezoid P’Q’R’S’. What are the coordinates of Trapezoid P’Q’R’S’?
The rule for reflecting across the line \(y=x\) is \((x,y)\rightarrow(y,x)\). When we apply the rule to the points of the vertices of Trapezoid PQRS, we get P’\((3,2)\), Q’\((3,6)\), R’\((1,8)\), S’\((1,0)\)
Rectangle LMNO has been reflected across a certain line to create Rectangle L’M’N’O’.
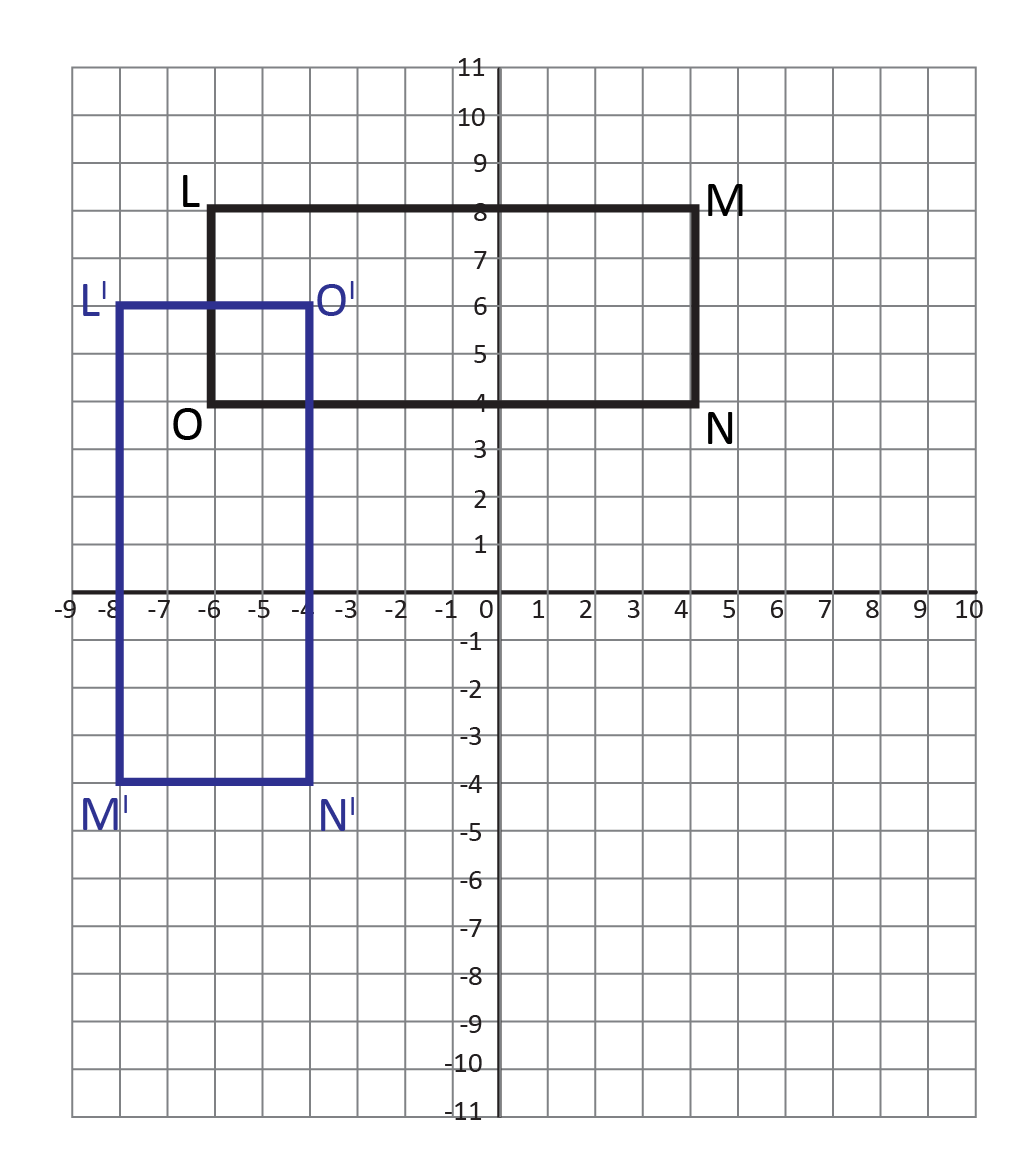
Which line was Rectangle LMNO reflected across?
We will start by looking at the coordinates of the vertices of rectangle LMNO and L’M’N’O’ next to each other. L\((-6,8)\rightarrow\)L’\((-8,6)\), M\((4,8)\rightarrow\)M’\((-8,-4)\), N\((4,4)\rightarrow\)N’\((-4,-4)\), and O\((-6,4)\rightarrow\)O’\((-4,6)\). When examined closely, we see that the rule that was applied here is \((x,y)\rightarrow(-y,-x)\), which is the rule for reflecting across the line \(y=-x\). It can also be thought of as reflecting across the line \(y=x\) and also reflecting about the origin, which is why the rule is \((x,y)\rightarrow (-y,-x)\).
Quadrilateral ABCD is shown on the coordinate grid. When quadrilateral ABCD is reflected across the origin, Quadrilateral A’B’C’D’ is created.
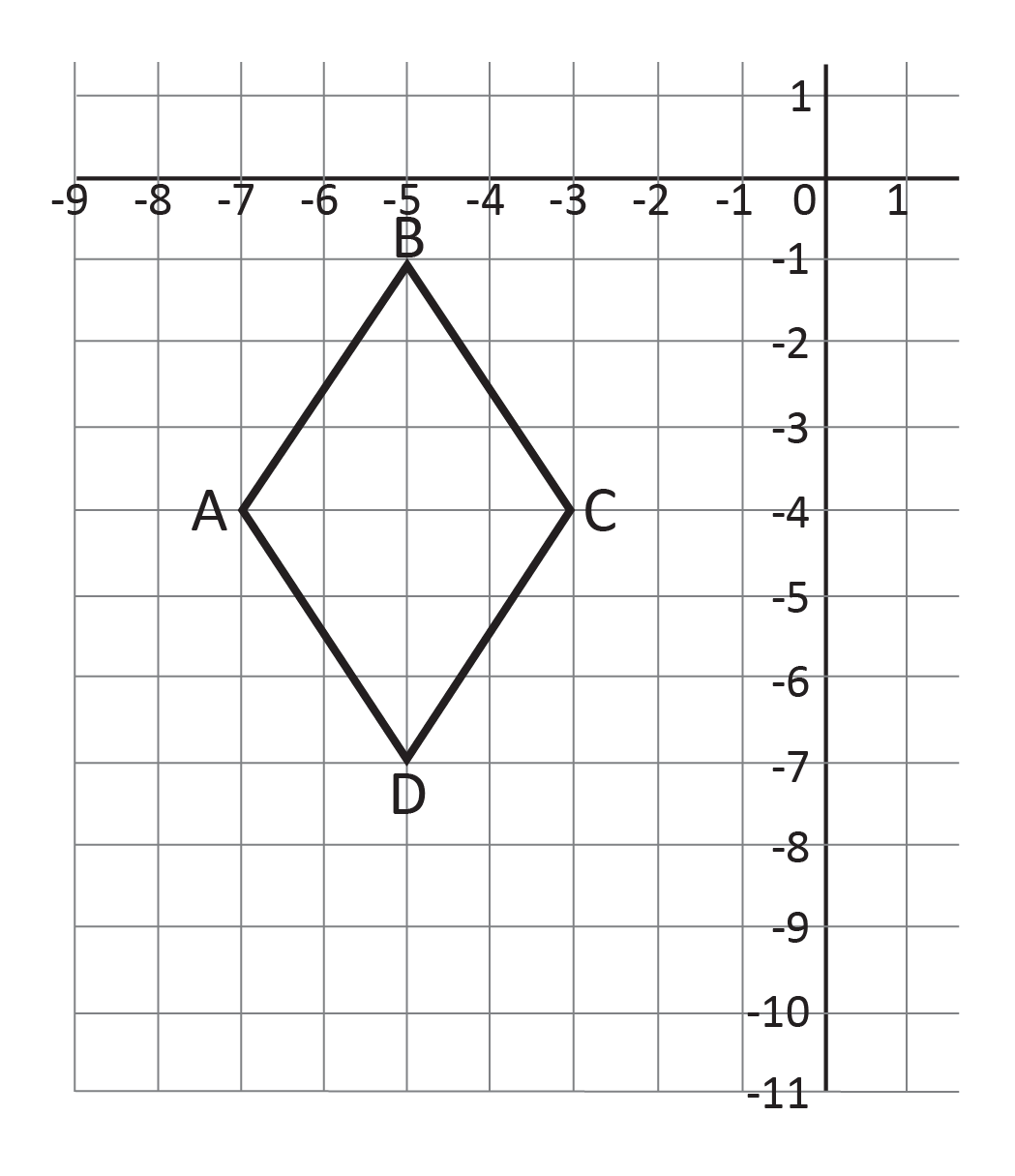
What are the coordinates of the vertices of Quadrilateral A’B’C’D’?
The rule for reflecting across the origin is \((x,y)\rightarrow (-x,-y)\). We will start by finding the vertices of Quadrilateral ABCD from the coordinate plane, which are A\((-7,-4)\), B\((-5,-1)\), C\((-3,-4)\), D\((-5,-7)\). When we apply the rule, we get A’\((7,4)\), B’\((5,1)\), C’\((3,4)\), D’\((5,7)\).
Triangle DEF, where D\((-6,2)\), E\((4,6)\), and F\((1,-2)\), is reflected across a certain line to create triangle D’E’F’ with coordinates D’\((6,2)\), E’\((-4,6)\), and F’\((-1,-2)\). Which line was the triangle reflected across?
We will start by comparing the original point with its reflected point and we can see that the value of the \(y\) coordinate stayed the same in all three vertices, but the value of the \(x\) coordinate has the opposite sign from the original. This is the rule we follow when we are reflecting across the \(y\)-axis, which is \((x,y)\rightarrow (-x,y)\).
