
Hi, and welcome to this video on projectile motion! Today, we’ll discuss what projectile motion is and break down some important concepts.
What is Projectile Motion?
Projectile motion occurs any time an object is thrown or launched into the air and falls back to the ground. With physics, it’s possible to predict things like where the object will land and the amount of time it will take for the object to reach the ground. Our ability to predict these values depends on the information we have about the scenario.
Trajectory
When you begin a projectile motion problem, the first thing you’ll have to do is think about the trajectory of the object. In other words, consider the direction the object is moving. Is all of the motion vertical, like an object falling to the ground? Or is the object launched or thrown at some angle?
It helps to draw out the trajectory if it isn’t already given to you. Even an approximation can be helpful in visualizing the situation. You’ll want to determine your starting point, end point, and the path of travel.
When we’re working with projectile motion, we are dealing with vectors like velocity and acceleration, which we break up into the \(x\) and \(y\) components. This is because the motion in the \(x\) and \(y\) components are independent of each other.
For example, at every point along the path of motion here, there is a velocity in the \(x\) direction and a velocity in the \(y\) direction. The \(x\) and \(y\) position changes along the path, with \(x_0\) and \(y_0\) marking the starting point.
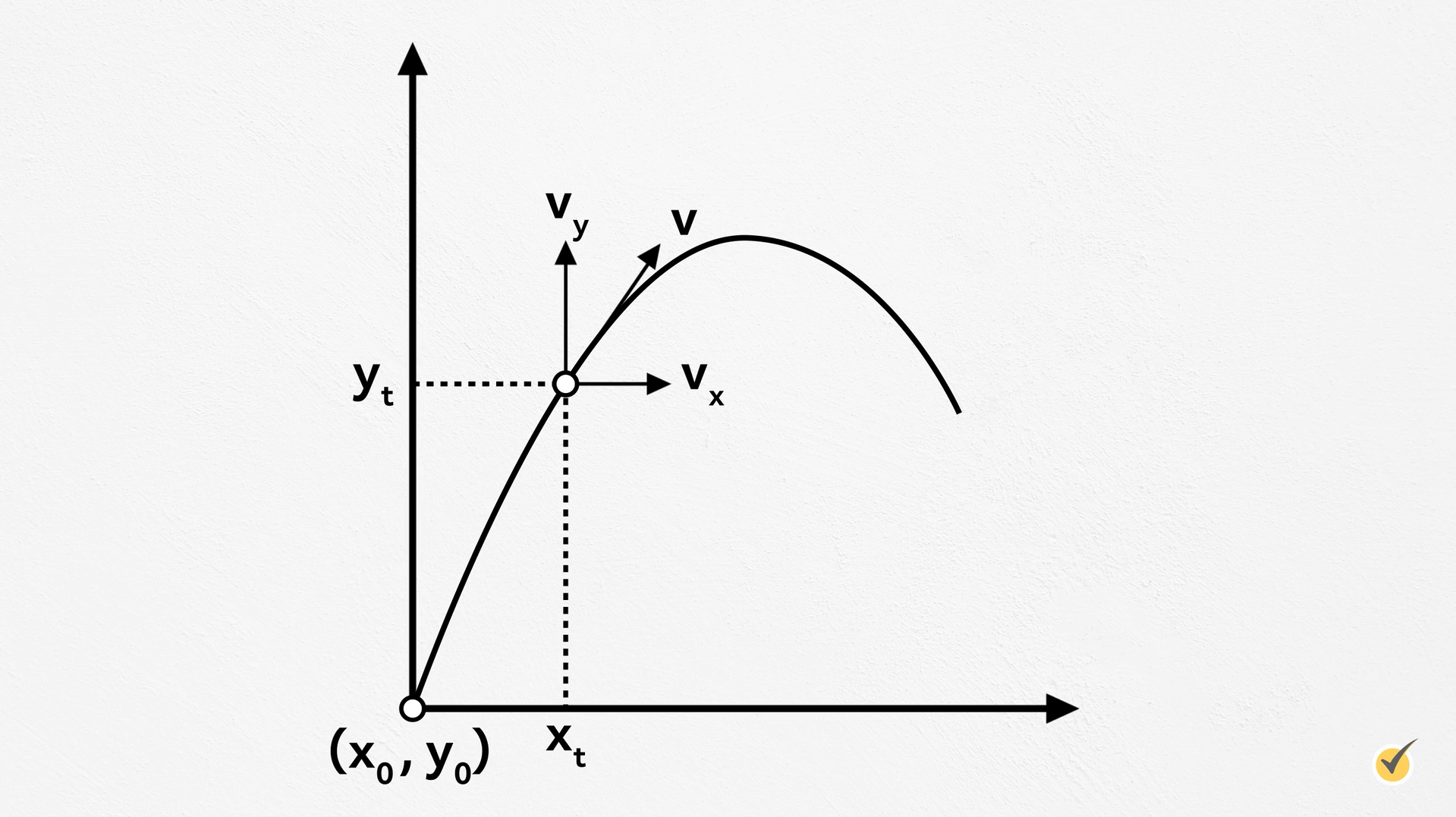
For every projectile motion problem we’ll have a set of variables in each direction. Let’s quickly go over what each of these variables are.
\(y\)-direction: \(y_0,y,v_{0y},v_y,a_y\)
\(x_0\) and \(y_0\) are the initial positions, \(x\) and \(y\) are the position vectors at the time you are solving for, \(v_{0x}\) and \(v_{0y}\) are the initial velocities in each direction, \(v_x\) and \(v_y\) are the ending velocities in each direction, and \(a_x\) and \(a_y\) are your accelerations in each direction. In addition to these variables, we have the time, \(t\), which is a scalar quantity.
Simplifications
So, there appears to be a lot to keep track of in these projectile motion problems! But, before you give up and throw out your physics book, check out these simplifications.
- In any basic projectile motion problem you encounter, gravity will be the only force you have to worry about since air resistance is usually negligible. This simplifies all of the acceleration variables. Gravity only acts in the \(y\)-direction, so \(a_x\) will always equal zero! And, assuming you’re talking about the Earth, any acceleration in the \(y\) direction will always be \(g=-9.8\text{ } m/s^2\). Note that it is negative since, by convention, we assign up to be the positive \(y\)-direction and gravity always acts down.
- In most cases, you will set up the problem so that \(x_0=0\) and in some cases where \(y_0=0\), as well. We’ll show an example in a moment where \(y_0\) is not zero.
- If you have a problem where the object is launched straight up into the air and falls back down or it is dropped from some height straight to the ground, then all of the motion is in the vertical direction and you won’t need to worry about any of the horizontal parameters.
Kinematic Equations
So how do you put all of these variables together to describe the motion of an object? You may have already been introduced to the kinematic equations.
With this set of equations and the handy tips we discussed, you can solve any projectile motion problem.
| Equations in \(x\)-direction | Equations in \(y\)-direction |
|---|---|
| \(x=x_{0}+v_{0x}t+\frac{1}{2}a_{x}t^{2}\) | \(y=y_{0}+v_{0y}t+\frac{1}{2}a_{y}t^{2}\) |
| \(v_{x}=v_{0x}+at\) | \(v_{y}=v_{0y}+at\) |
| \(v_{x}^2=v_{0x}^{2}+2a(x-x_{0})\) | \(v_{y}^2=v_{0y}^{2}+2a(y-y_{0})\) |
| \((x-x_{0})=\frac{1}{2}(v_{x}+x_{0x})t\) | \((y-y_{0})=\frac{1}{2}(v_{y}+y_{0y})t\) |
Don’t worry; you won’t have to use all of these equations for every problem! The trick to these problems is to be methodical. It helps to follow these steps:
- Read the problem and draw out a free body diagram if there isn’t one given.
- Determine which variables you already know.
- Determine which variable you need to calculate.
Example Problem
Let’s look at an example of one of the most common kinds of projectile motion problems.
Imagine you kick a ball off a cliff at a speed of 12 meters per second. The ball goes straight along the ground until it is over the cliff, which is 30 meters high. How long does it take for the ball to land? How far away does the ball land?
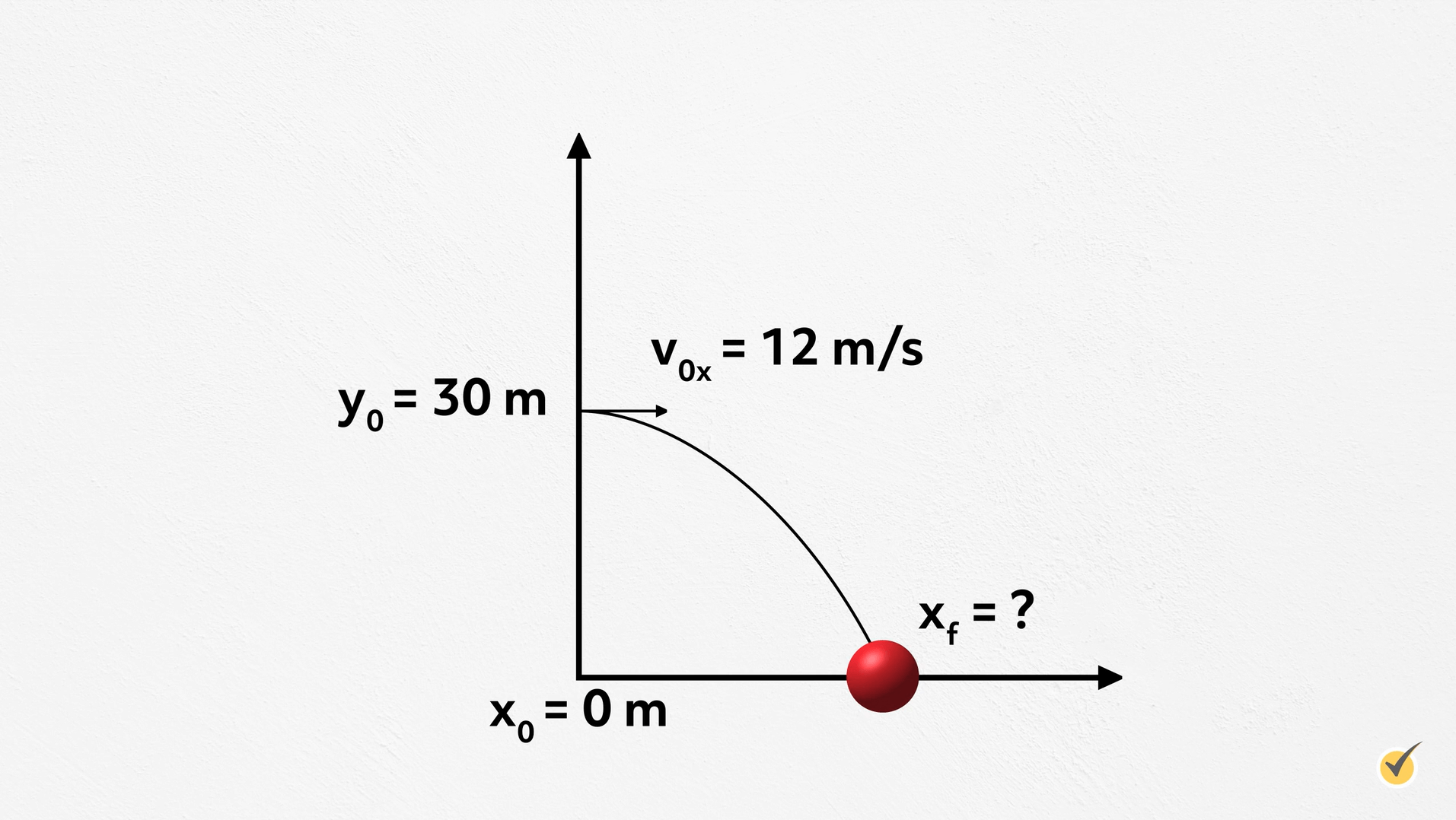
We are told that the ball moves along the ground and goes straight off the cliff at 12 meters per second. This means that the initial velocity, \(v_o\), is only in the \(x\) direction and is 12 meters per second. So, we have \(v_{ox}=12\text{ }m/s\) and \(v_{oy}=0\). We also know that \(y_o=30\) meters, and we’ll set \(x_o\) to equal \(0\).
As with most projectile motion problems, gravity is the only force we need to worry about, so the only acceleration is \(g=-9.8\text{ }m/s^{2}\). Remember, this is only in the \(y\) direction and only after the ball is over the cliff. So, \(a_y=-9.8\text{ }m/s^{2}\), which is 0 in the \(x\) direction.
Now, what do we need to find?
We are asked for the time, \(t\). If we look back at our kinematic equations, we can figure out which equation to use to get the time it takes for the ball to hit the ground.
It looks like we have everything but \(t\) for \(y=y_o+v_{ov}t+\frac{1}{2}a_vt^{2}\).
If we plug in \(v_{oy}=0,y_o=30m\), and \(y=0\), and \(a_y=-9.8\text{ }m/s^{2}\) (negative because it is pulling the ball in the negative y direction) we get a simpler equation, \(0=30+\frac{1}{2}(-9.8)t^{2}\).
First, subtract 30 from both sides of the equation,
To get rid of the \(\frac{1}{2}\), just multiply both sides by 2.
Then, divide both sides by -9.8 to get
Then, just take the square root of both sides to get t ≈ 2.5 seconds. This seems like a reasonable answer. It should only take a few seconds for a ball to fall 30 meters.
Now, we can find how far away the ball lands. Looking back at our equations, it makes sense to use the same equations, but for the \(x\) components this time.
Remember, there is no acceleration in the \(x\) direction, so that is zero, eliminating the last term.
\(x=x_o+v_{ox}t\)
But, we said \(x_o=0\), as well. So plugging in what we know, we get:
The ball lands about 30 meters away from the cliff.
Another type of projectile motion problem involves the object being shot upward into the air at an angle before falling back down. In this case, the initial velocity has both an \(x\) and \(y\) component and you’ll have to use simple trigonometry to determine \(v_{0x}\) and \(v_{0y}\).
Practice Questions
Now that we’ve gone through a thorough overview of projectile motion, let’s test your knowledge with a few practice problems!
1. Imagine throwing a rock straight up into the air at a vertical velocity of 4 m/s, so that it goes up to a height of 2 meters before it falls back down into your hand. Is there any point in the rock’s trajectory that its vertical velocity is zero?
- No, it gets faster and faster for the whole trajectory.
- Yes, halfway through its trajectory, when it changes direction.
- No, it stays at 4 m/s the entire time.
2. If a cannon launches a cannonball into the air at an angle of 45° from the ground at an initial velocity of 35 m/s, the initial velocity will have both an \(x\) and \(y\) component, \(v_{ox}\) and \(v_{oy}\). We know that the vertical velocity will change due to the acceleration due to gravity. Will the horizontal velocity change throughout the cannonball’s trajectory?
- No, there are no forces in the horizontal direction and that means there is no acceleration.
- Yes, if the vertical component changes, then the horizontal component must change too.
- No, but it might change if the angle were different.
That’s all for this review! Thanks for watching, and happy studying!