Derivative Properties and Formulas

“Property” is a mathematical term for an identity or a true statement which can simplify a problem. For example, one of the exponent properties is that \(a^{x}a^{y}=a^{x+y}\). In this video, we are going to go over some derivative properties that will help simplify many of the problems you’ll come across.

The first derivative property we are going to cover is called the Constant Rule, which states that the derivative of any constant is zero.

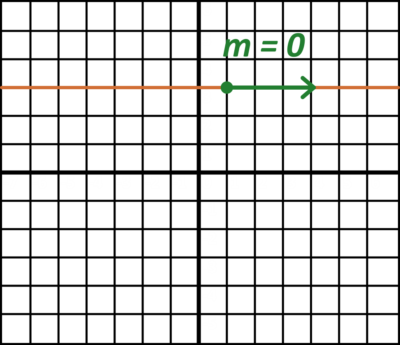
This makes sense, because if we graph a constant function, such as \(f(x)=3\), we get a horizontal line. Because the line is horizontal, the slope at all points is zero. This is true no matter what point we pick, whether large or small, positive or negative. As long as we are just talking about a constant, the derivative is zero.

The next property to consider is that we can factor out constants from derivatives. For example, we already know that the derivative of \(3x^{2}\) is \(6x\), because the Power Rule tells us to multiply by the starting exponent and then reduce the power by one.

Another way to think of this, though, is that we can pull that 3 out to the front of the derivative…

…take the derivative of \(x^{2}\) by itself…

…and simplify to get the same result.

Of course, in this example, it’s faster to just multiply 3 by 2 and reduce the power without the intermediate factoring step. But with trickier derivatives, like \(\frac{d}{dx}\frac{5x^{3}}{3}\), this property can be helpful. To take this derivative, notice that we can factor out the 5 from the top and the 3 from the bottom as \(\frac{5}{3}\). Then we can handle \(x^{3}\) by itself.

The derivative of \(x^{3}\) is \(3x^{2}\), so we will write that now.

From here, the 3s cancel and we are left with \(5x^{2}\). If you see a derivative problem with a coefficient—even a fractional one—you can use this factoring property to simplify the problem.

The third and final derivative property we are going to cover in this video is the Sum and Difference Rule. You will likely come across many derivative problems that involve functions with multiple terms. For example, you may be asked to find the derivative of \(f(x)=x^{2}+4x-5\). There’s nothing to fear with such problems, though, because these derivatives can be handled one term at a time. The derivative of the first term, \(x^{2}\), is \(2x\). The second term’s derivative is 4, and the third term’s derivative is zero because it is simply a constant. So \(f'(x)\) is the sum of each term’s derivatives, which gives us:

The formal way of expressing the Sum and Difference Rule is that the derivative of many terms is equal to the sum (or difference, if the terms are subtracted) of each term’s derivative.

Let’s quickly review what we’ve discussed in this video. First, the Constant Rule tells us that the derivative of any constant is always 0. Second, we learned that some derivatives can be made easier by factoring out a constant and handling the remaining function on its own.

Finally, the Sum and Difference Rule states that the derivative of a function with many terms is simply the sum or difference of the individual terms’ derivatives.

I hope this video was helpful. Thanks for watching, and happy studying!