At first, the term “consecutive interior angles” may seem intimidating. However, try breaking it down word-by-word:
- To be consecutive means to ‘sit’ next to each other (or follow one another).
- Something that is interior is contained in between other things.
- An angle is a space measured between two intersecting lines.
In order to observe consecutive interior angles, we need to have two lines (they could be parallel or they could eventually intersect) that are both intersected by a third, transversal line.
We start with the two lines, \(\overleftrightarrow{x}\) and \(\overleftrightarrow{y}\).
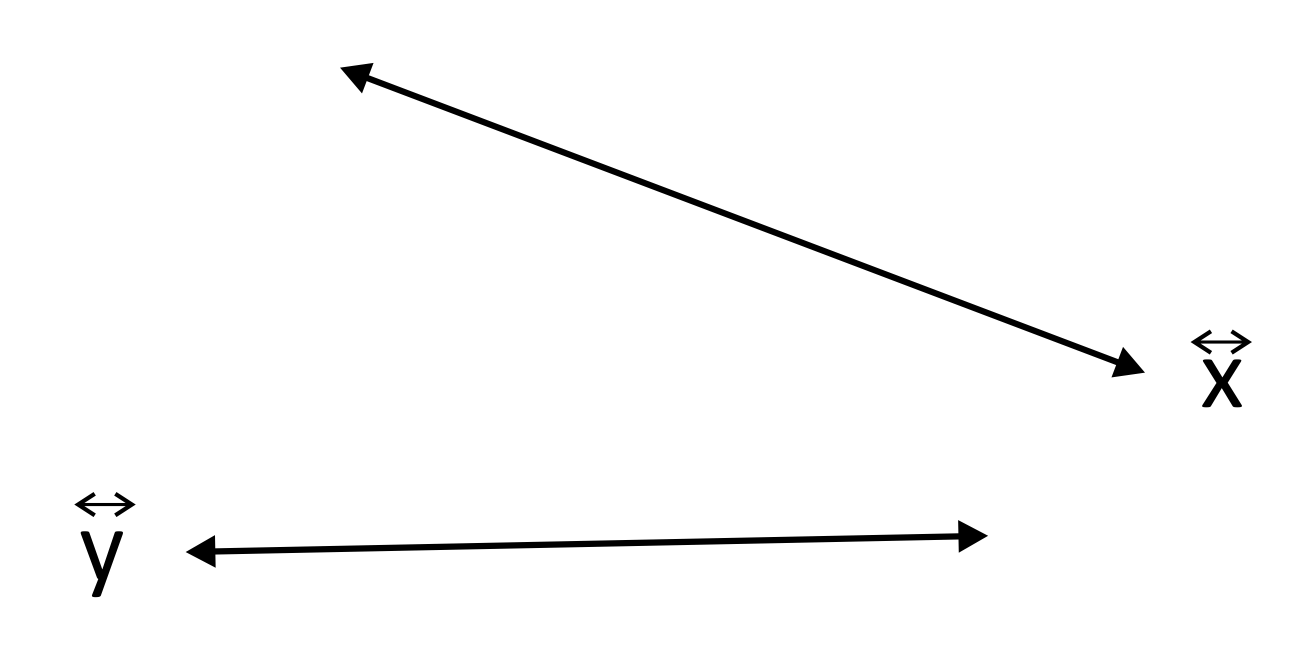
And now a transversal line, \(\overleftrightarrow{T}\), is crossing both original lines.
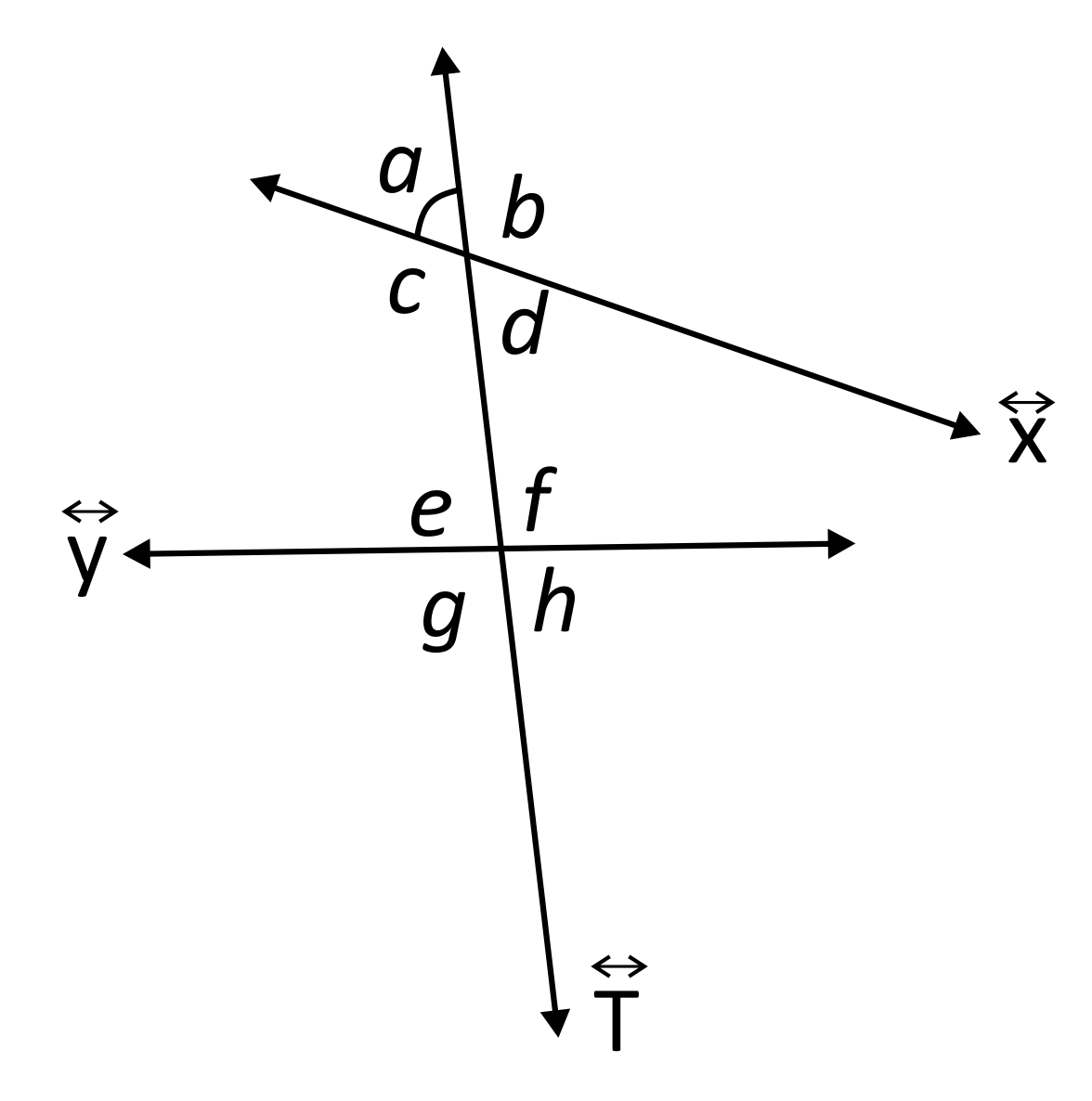
Notice that there are 8 angles total in this scenario. Any angle that sits in between line \(\overleftrightarrow{x}\) and line \(\overleftrightarrow{y}\) is an interior angle. Hence, in the above example, \(∠c,∠d,∠e,\) and \(∠f\) are all interior angles.
Now, let’s look into consecutiveness:
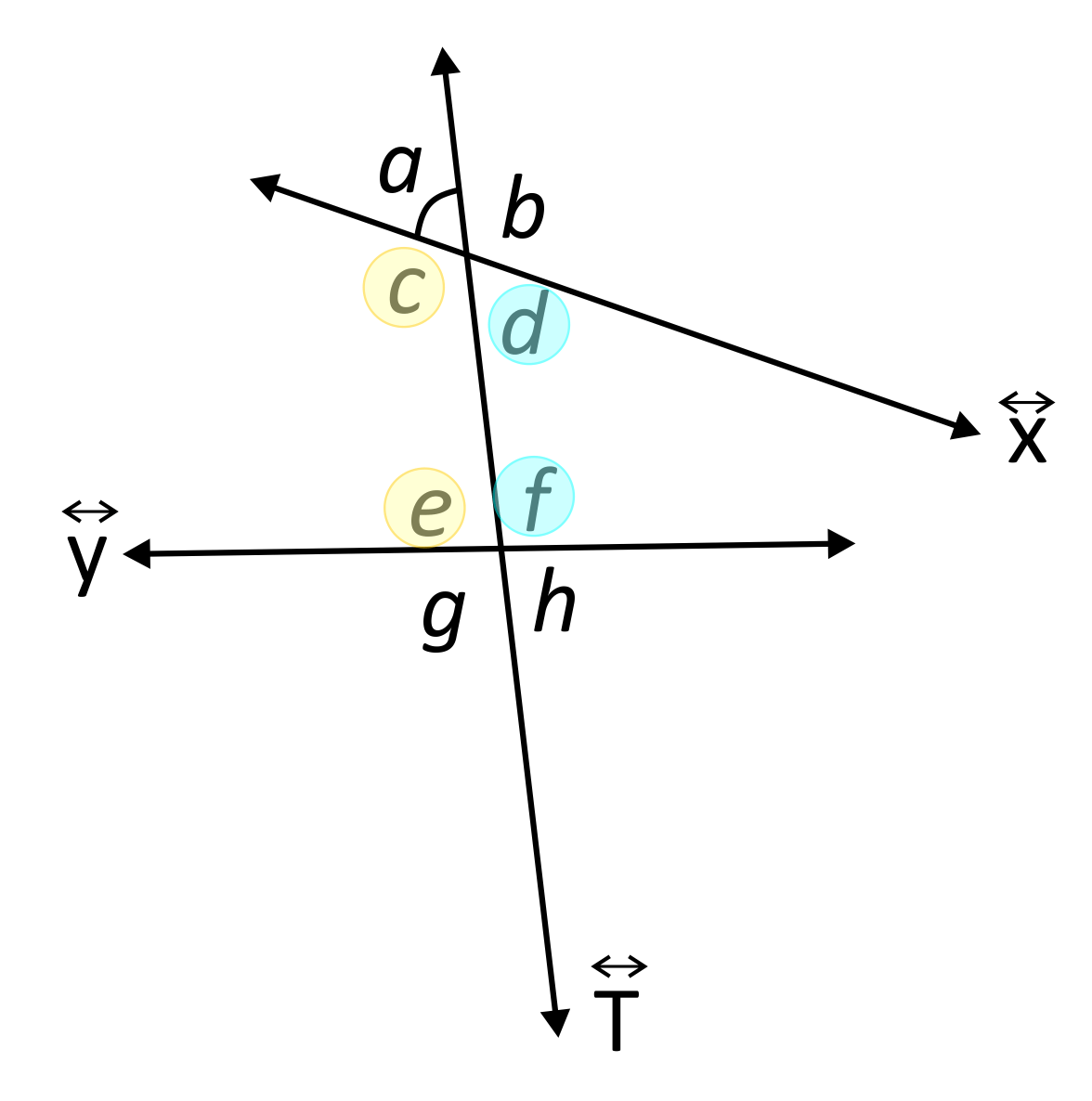
When dealing with consecutive interior angles, it’s important to understand that the word, “consecutive,” is in respect to the transversal line. So, if two angles sit next to each other on the same side of the transversal, they are considered consecutive.
This all leads us to the following conclusions: the pair \(∠c\) and \(∠e\) are consecutive interior angles, and- similarly- \(∠d\) and \(∠f\) are consecutive interior angles as well.
Note that \(∠c\) and \(∠f\) ARE NOT consecutive interior angles; neither are \(∠d\) and \(∠e\), because neither pair sits on the same side of \(\overleftrightarrow{T}\) together.
When discussing angles on any number of intersecting lines, we have to understand what supplementary angles are. By definition, when the measures of two angles sum up to 180°, we call the pair “supplementary.” In fact, if any two angles form a linear pair (see below), then they are supplementary.
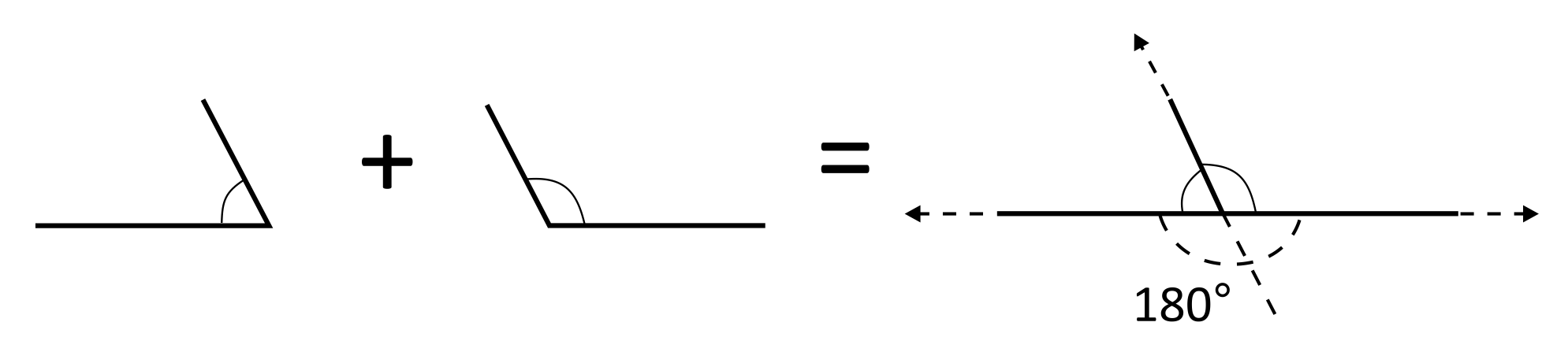
This concept is called the linear pair postulate, and it is a key piece in understanding the Consecutive Interior Angles Theorem:
Let’s prove that \(∠c\) and \(∠e\) are supplementary.
We’re given the parallel lines, \(\overleftrightarrow{x}\) and \(\overleftrightarrow{y}\), with the intersecting transversal, \(\overleftrightarrow{T}\).
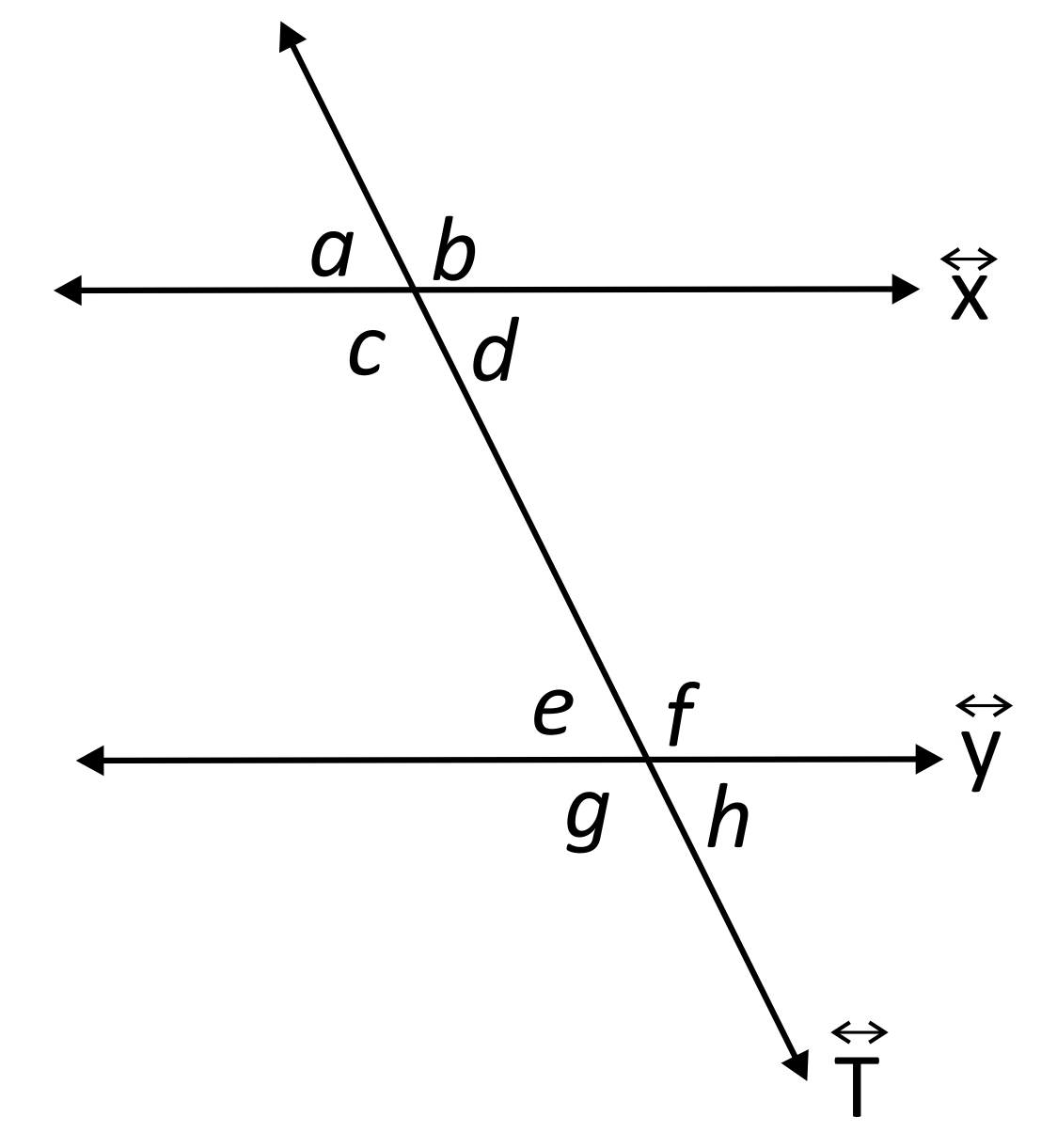
By the corresponding angle postulate, we know that \(∠a\) and \(∠e\) are congruent- meaning: \(m∠a=m∠e\) (which reads as “the measure of angle \(a\) equals the measure of angle \(e\)”).
We also know by the linear pair postulate that \(m∠c+m∠a=180°\). We can substitute \(m∠e\) for \(m∠a\): \(m∠c+m∠e=180°\).
Hence, by definition, \(∠c\) and \(∠e\) are supplementary.
Here’s a simpler form of that proof:
| \(\overleftrightarrow{x} \parallel \overleftrightarrow{Y}\) | Given |
| \(∠a≅∠e\) | By the corresponding angle postulate |
| \(m∠a=m∠e\) | By the definition of congruence |
| \(∠a\) and \(∠c\) are supplementary | By the linear pair postulate |
| \(m∠c+m∠a=180°\) | By the definition of supplementary angles |
| \(m∠c+m∠e=180°\) | By the property of substitution |
| \(∠e\) and \(∠c\) are supplementary | By the definition of supplementary angles |
Consecutive Interior Angles Sample Questions
Here are a few sample questions going over consecutive interior angles.
What two pairs of angles are consecutive interior angles?
\(∠I\) & \(∠V\) and \(∠III\) & \(∠VII\)
\(∠III\) & \(∠VI\) and \(∠IV\) & \(∠V\)
\(∠III\) & \(∠V\) and \(∠IV\) & \(∠VI\)
\(∠I\) & \(∠VII\) and \(∠II\) & \(∠VIII\)
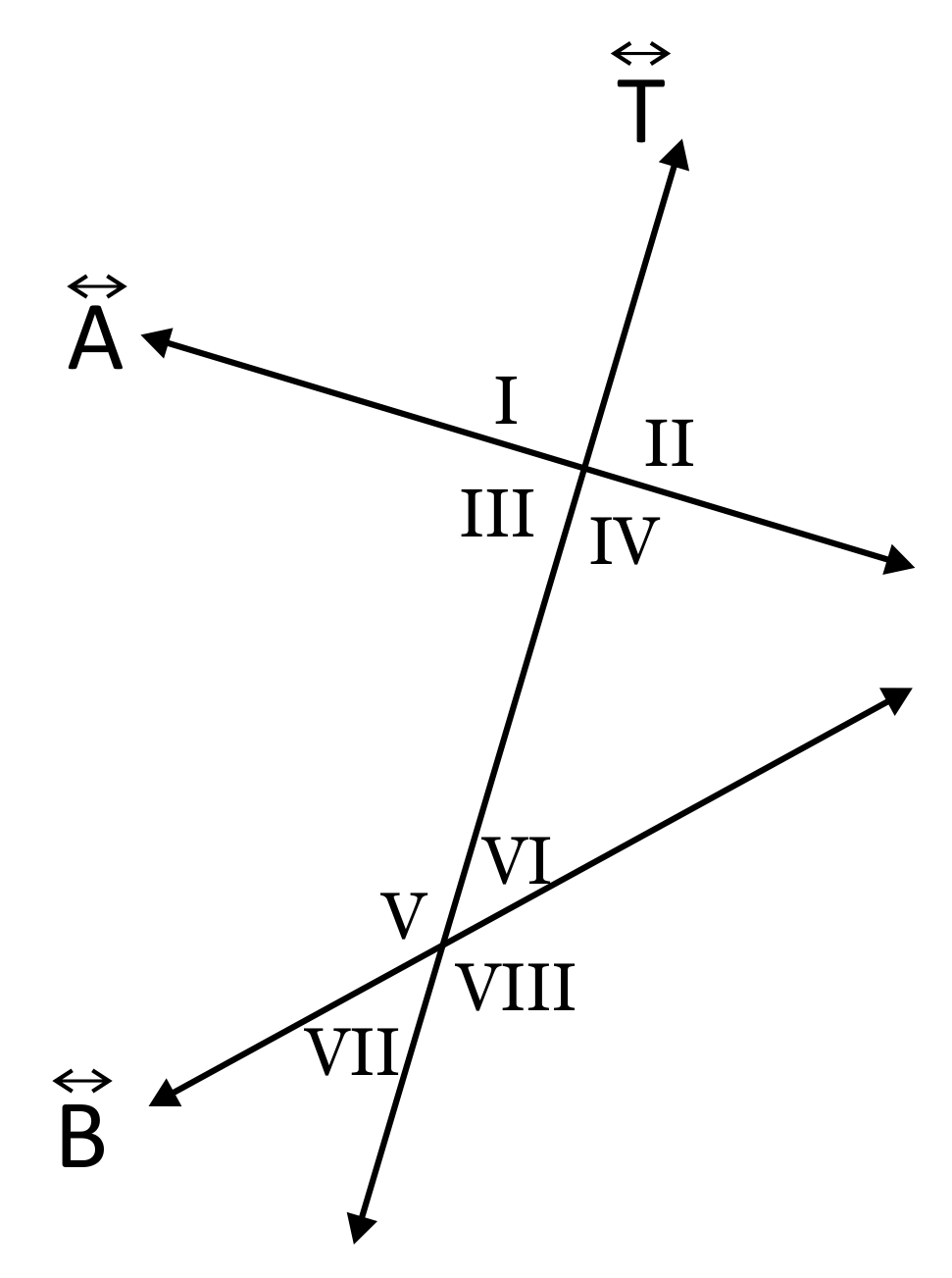
The angles \(∠III\) & \(∠V\) are both ‘inside’ \(\overleftrightarrow{x}\) and \(\overleftrightarrow{y}\), and they sit next to each other on the same side of \(\overleftrightarrow{T}\). The same is true for the pair \(∠IV\) & \(∠VI\).
True or False: \(∠z\) and \(∠w’\) are consecutive interior angles.
True
False
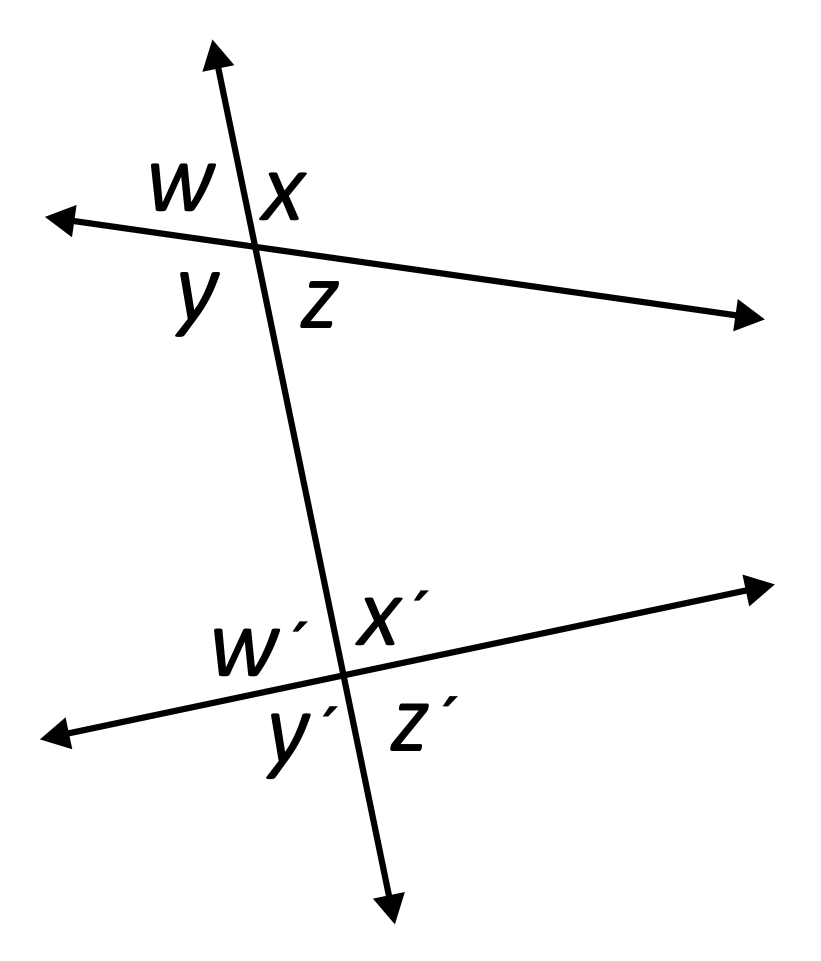
Both \(∠z\) and \(∠w’\) are interior angles, but they are not consecutive to one another. \(∠y\) & \(∠w’\) are consecutive interior angles, and \(∠z\) & \(∠x’\) are too.
True or False: The two labeled angles are supplementary.
True
False
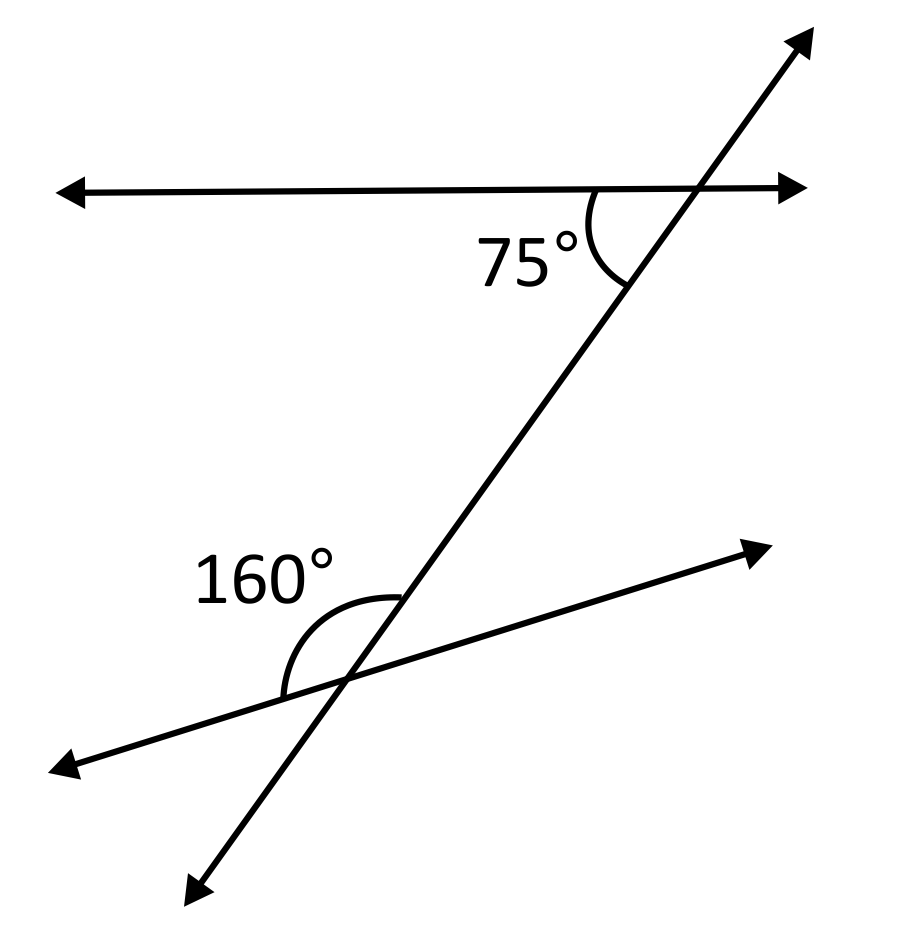
\(75°+160°=235°≠180°\). Thus, by definition, these angles are not supplementary.
True or False: Angles \(∠u\) and \(∠w\) are supplementary, consecutive interior angles.
True
False
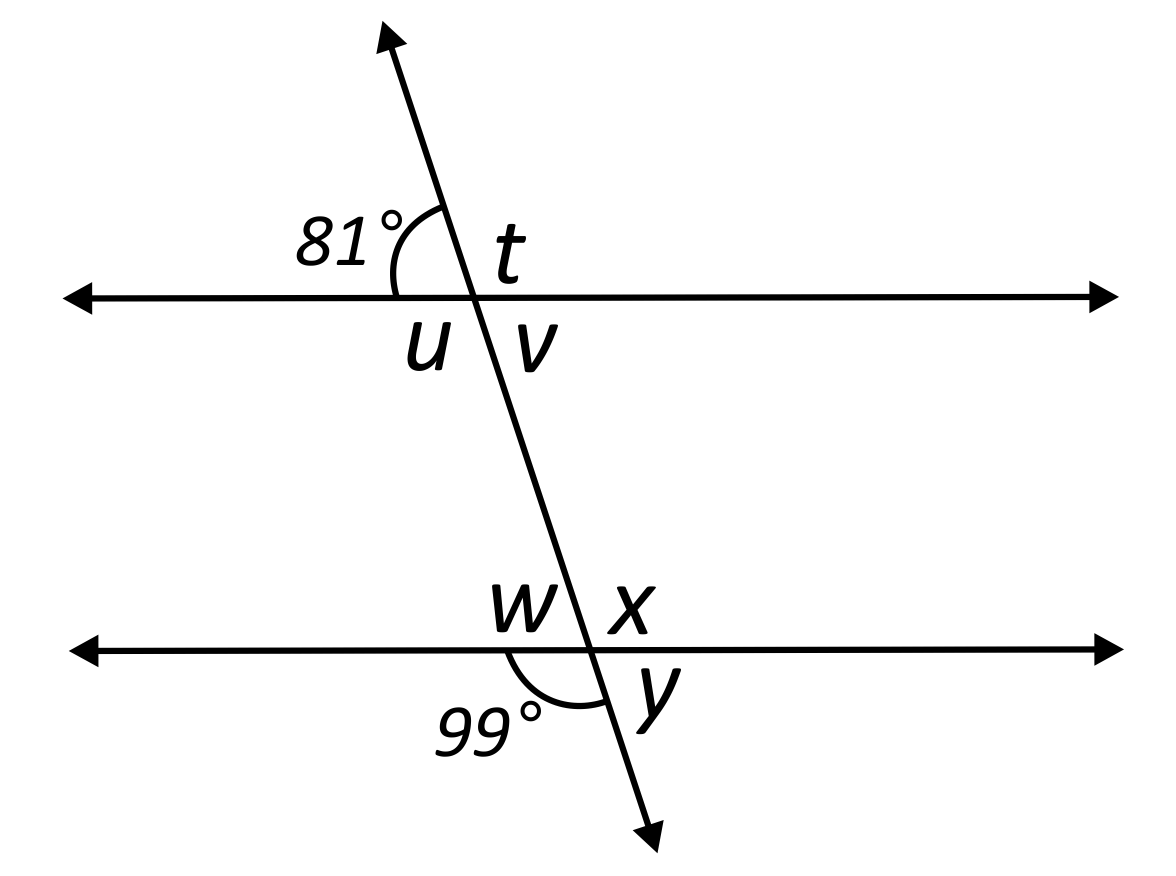
\(∠u\) and \(∠w\) are consecutive interior angles, and they are supplementary. By the linear pair postulate, we know that \(m∠u=180°-81°=99°\). We also know, thanks to the corresponding angle postulate and the definition of congruence, that \(m∠w=81°\). Hence, \(m∠u+m∠w=99°+81°=180°\).
Of the labeled angles, which pair is a set of supplementary, consecutive interior angles?
\(∠2\) & \(∠4\)
\(∠2\) & \(∠3\)
\(∠1\) & \(∠3\)
\(∠1\) & \(∠5\)
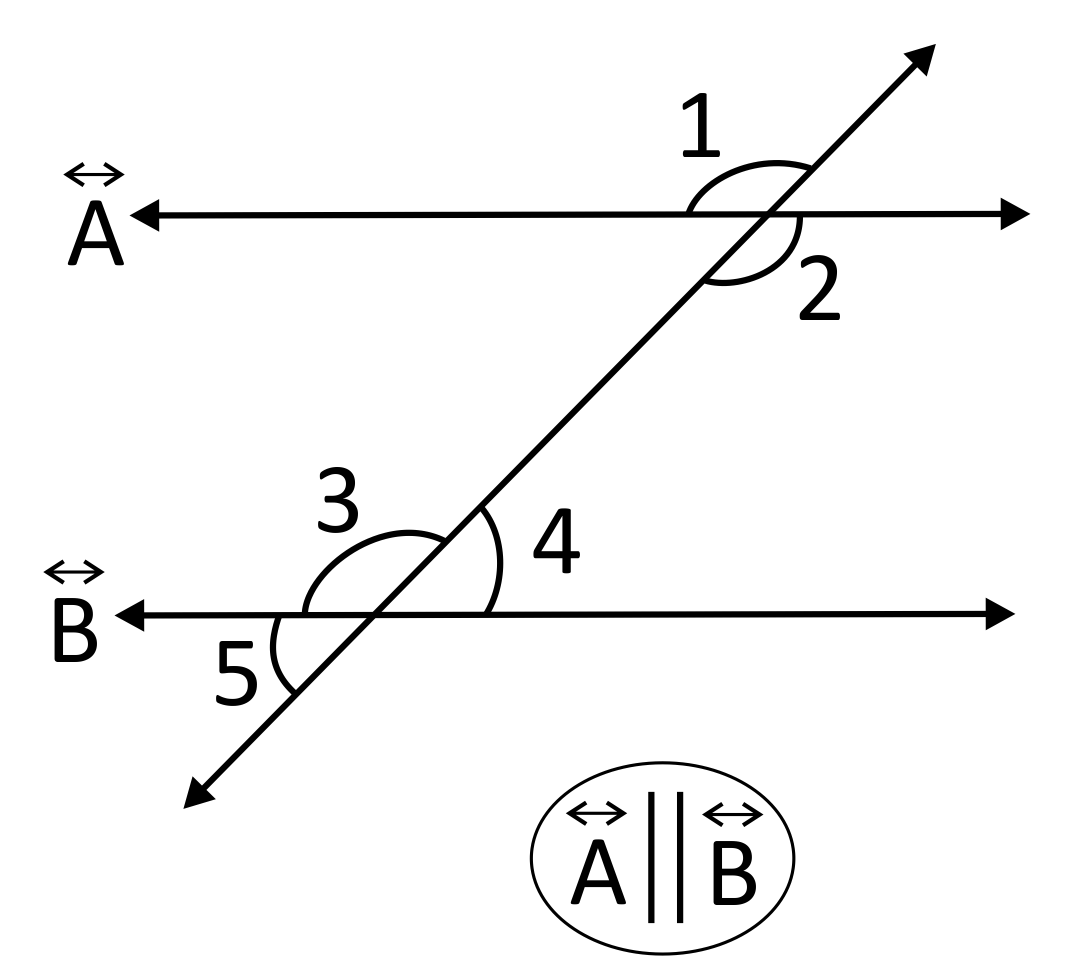
\(∠2,∠3,\) and \(∠4\) are all interior angles; but \(∠2\) and \(∠4\) are consecutive interior angles. Additionally since we know that \(\overleftrightarrow{A}\) and \(\overleftrightarrow{B}\) are parallel \((\overleftrightarrow{x} \parallel \overleftrightarrow{Y})\) by the consecutive interior angles theorem, we also know that \(m∠2+m∠4=180°\). Thus, \(∠2\) and \(∠4\) are supplementary angles as well.