
Today, we’re going to take a look at conditional probability. This type of probability is all about finding the odds of something happening given that something else has already occurred.
Review of Basic Probability
Let’s start with a refresher on basic probability. The probability of something happening can be expressed as the number of desired outcomes divided by the number of total possible outcomes:
Example #1
Here’s an example of a basic probability problem. There are 10 marbles in a bag: three are blue, three are red, and four are orange. What are the odds of pulling out a red marble?
To solve this, we’d place the number of desired outcomes on the top (in this case, it’s 3 because there are three red marbles) and the total number of possible outcomes on the bottom (this is 10 since there are 10 total marbles in the bag).
Seems pretty straightforward, right?
Conditional Probability
Well, conditional probability adds a bit of a twist to this, as the objects or people in question often have more than one possible attribute.
Example #1
Let’s look at an example problem with more than one possible attribute.
Out of 100 houses sold, 50 had a garage, 40 had a pool, and of these, 10 had both a garage and a pool, leaving 20 houses with neither. Given that a house had a garage, what are the odds that it also had a pool?
What do we do with all this information? If we draw it as a Venn diagram, we can make more sense of it:
We can now see the overlap between the houses sold with garages and the houses sold with pools, all within the larger set of houses sold. It’s easier to see now that of the 50 houses sold with a garage, 10 of them also had a pool. So the odds are \(\frac{10}{50}\), which can be expressed as the fraction \(\frac{1}{5}\), or 20%.
Fortunately, there’s a faster way to do this than by drawing a diagram every time you encounter a conditional probability question.
Conditional Probability Formula
There’s a handy formula we can use:
We read this formula as “the probability P of event B happening given that event A has happened is equal to the probability of events B and A both happening over the probability that event A has happened.”
In these types of problems, both probabilities on the right side of the equation are usually given or can be determined from a sentence or table. So in our sample problem, the \(P(B|A)\) is the 10 houses that were sold with both a garage and a swimming pool, out of the total 100 houses. This fraction can be written as \(\frac{1}{10}\).
The P(A) is the probability of a house being sold with a garage (event A), which is 50 houses out of the 100, or \(\frac{5}{10}\). Now that our formula is complete, we can divide \(\frac{1}{10}\) by \(\frac{5}{10}\) and we get \(\frac{1}{5}\), which is equal to 20%, just as we figured out from our diagram.
Example #2
Let’s try one more with numbers that aren’t quite so neat.
In a small town, there are 216 men: 144 of them have brown hair and 56 of them have mustaches. 24 of the men have brown hair and mustaches. What are the odds that a man chosen at random has a mustache given that he has brown hair?
Let’s plug into our formula. The probability of event A (brown hair) and event B (mustache) is the 24 men with both, divided by the 216 total men.
The probability of event A is 144 divided by the 216 total men. We divide \(\frac{24}{216}\) by \(\frac{144}{216}\) using fraction division. The 216s can be canceled out, so we are left with \(\frac{24}{144}\). This fraction can be reduced to \(\frac{1}{6}\), or ≈16.67%.
All right, that’s all for this review. I hope this increased your odds of understanding conditional probability.
Thanks for watching, and happy studying!
Conditional Probability Practice Questions
What is the formula for conditional probability?
The conditional probability formula allows us to determine the probability that Event B will occur, given the knowledge that Event A has already occurred. \(P(B|A)\) stands for “the probability of B given A.” The probability of Event B can be determined by dividing the probability of Events A and B occurring by the probability of Event A occurring.
The Venn diagram below shows sections for the probability of Event A occurring and the probability of Event B occurring. What does the shaded middle section represent?
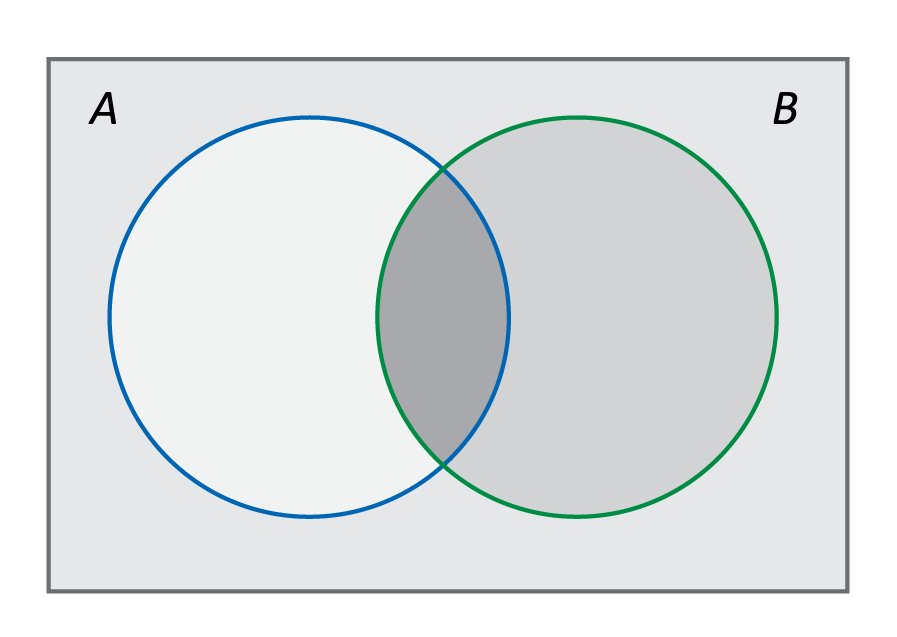
The middle section of the Venn diagram represents the overlap of Events A and B, where both events occur.
Which Venn diagram represents the following scenario:
100 customers have purchased cars at Jason’s car dealership this year. 40 of those customers purchased cars with touch-screen GPS, and 30 customers purchased cars with snow tires. 20 customers purchased cars with both touch-screen GPS and snow tires.
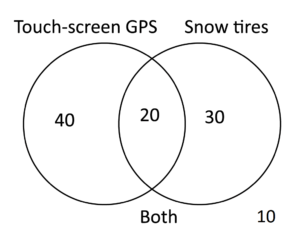
The far left portion of the Venn diagram represents the customers who purchased cars with touch-screen GPS but no snow tires. The far right portion of the Venn diagram represents the customers who purchased cars with snow tires but not touch-screen GPS. The middle section represents customers who purchased cars with both touch-screen GPS and snow tires.
Consider the same group of 100 customers from Jason’s car dealership. 40 purchased GPS, 30 purchased snow tires, and 20 purchased both. If a randomly selected customer has purchased the GPS, what would the probability be that they also purchased the snow tires?
The conditional probability formula can be used to solve this problem. The probability of Event A occurring (customer purchasing GPS) is 40 out of 100 customers, or 0.4. The probability of Event B occurring (customer purchasing snow tires) is 30 out of 100, or 0.3. The probability of a customer purchasing both, or Event A and B occurring, is 20 out of 100, or 0.2.
We know P(A) = 0.4 and P (A and B) = 0.2 so we can plug these into the formula.
\(P(A)=\frac{P(A \text{ and } B)}{P(A)}\) becomes \(P(B|A)=\frac{0.2}{0.4}\), which simplifies to 0.5, or 50%.
Sybil took two science tests. The probability of her passing both tests is 0.6 and the probability of her passing the first test is 0.8. What is the probability of her passing the second test if she passed the first test?
The conditional probability formula can be used to solve this problem. The probability of Event A occurring (passing the first test) is 0.8. The probability of Event A and B occurring (passing both tests) is 0.6.
We know \(P(A)=0.8\) and \(P(A\text{ and }B)=0.6\) so we can plug these into the formula.
\(P(B|A)=\frac{P(A\text{ and }B)}{P(A)}\) becomes \(P(B|A)=\frac{0.6}{0.8}\) which simplifies to 0.75 or 75%.
