Calculations Using Points on a Graph

Hello and welcome to this video about calculations using points on the coordinate plane!

So first off, let’s remember that a one-dimensional number line is a representation of all real numbers that extends infinitely in both the positive and negative directions and looks something like this:

When two number lines intersect at a right angle at their 0 coordinates, the two-dimensional coordinate plane is formed, which typically looks something like this:

Generally, the horizontal axis is called the \(x\)-axis and the vertical axis is called the \(y\)-axis. The point where the axes intersect is called the origin. Let’s plot a point on the coordinate plane.

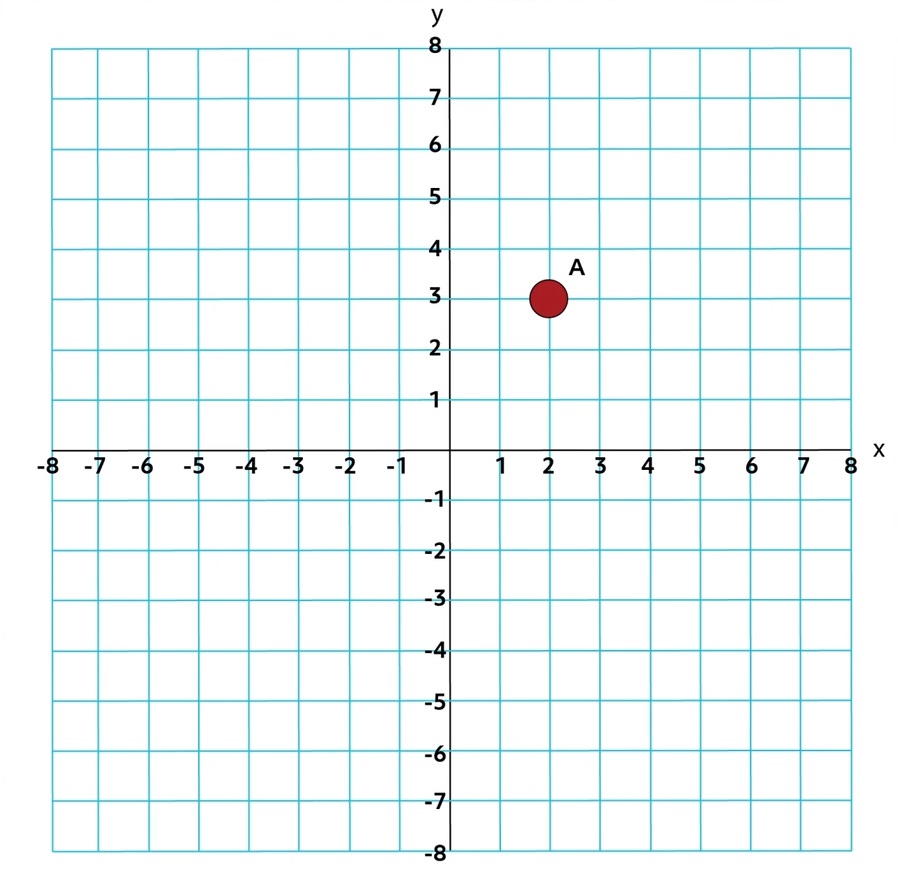
The location of Point A is given as a horizontal component (\(x\)) and a vertical component (y) and written as \((x,y)\). From the origin, to get to Point A, we would count two units to the right and three units up. So, the coordinates of Point A are \((2,3)\). Likewise, the coordinates of the origin are \((0,0)\).

Since the coordinate plane is comprised of number lines, they can be viewed “zoomed in” or “zoomed out” as much as necessary to convey data or a story. For example, the \(x\)-axis here has been “zoomed in”:

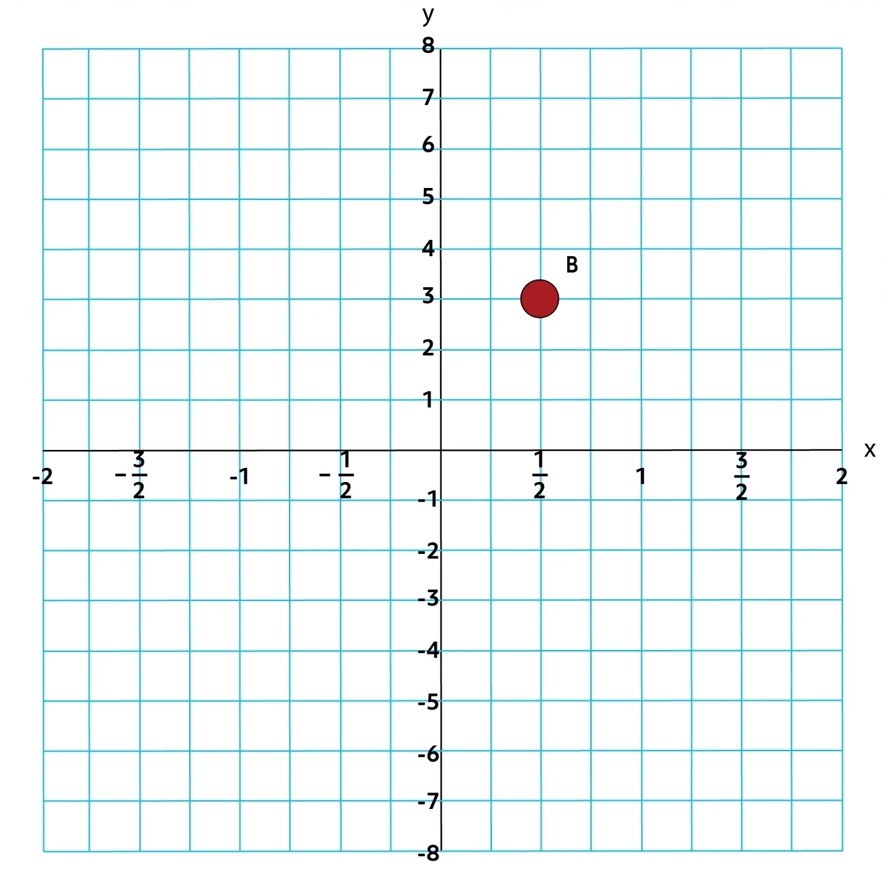
Because of the scale of the \(x\)-axis, the coordinate points of Point B are \((\frac{1}{2},3)\).

And the \(x\)-axis has been zoomed in here, while the \(y\)-axis has been zoomed out:

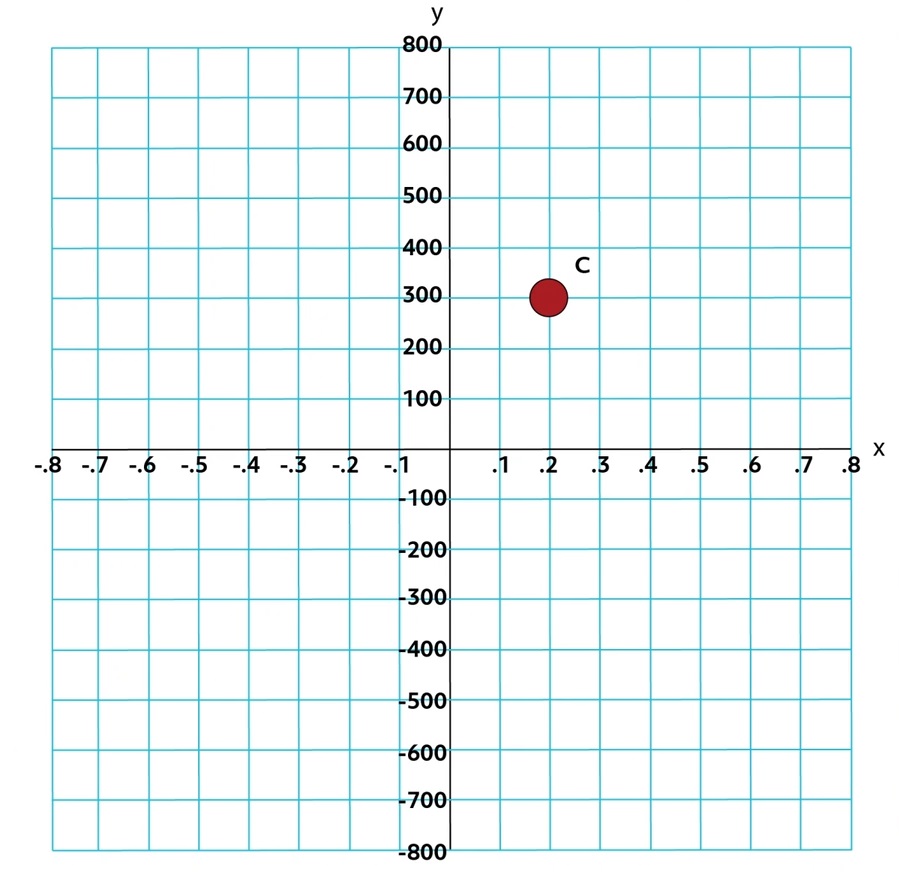
Because of the scales of the axes, the coordinates of Point C are \((0.2,300)\).

Using the coordinates of points on a coordinate plane, we can calculate the distance between two points.

The distance formula (an application of the Pythagorean theorem) looks like this:

\(D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)

In words, it’s “the square root of the horizontal distance squared plus the vertical distance squared.”

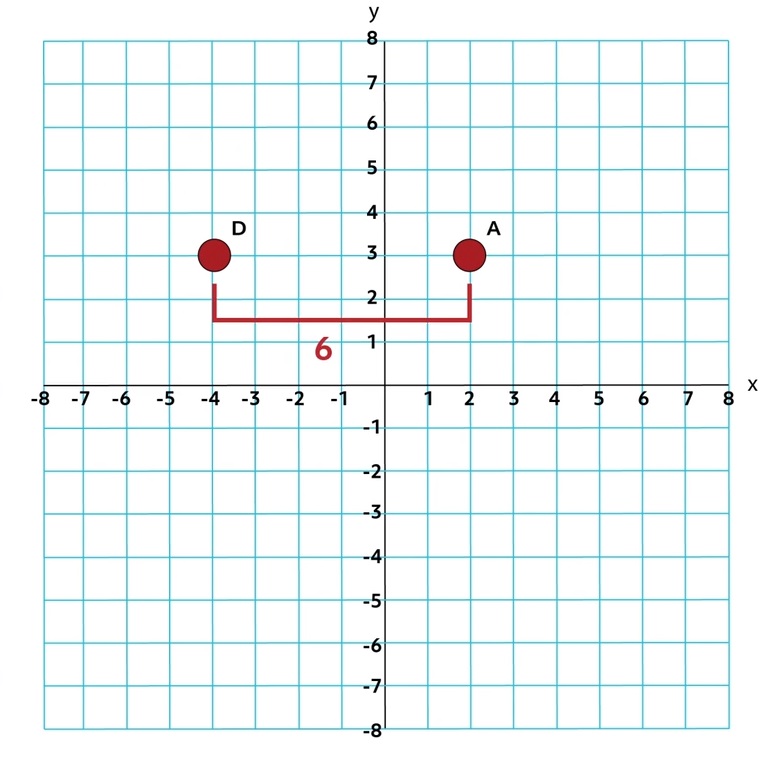
In this case, the formula can be used, but since Points A and D lie on the same horizontal gridline, all we need to do is count squares (this also works for two points on the same vertical gridline). The distance from Point A to Point D is 6 because the two points are 6 squares apart.

Using the formula yields the same result:

\(D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
 
\(D=\sqrt{(2-(-4))^2+(3-3)^2}\)
 
\(D=\sqrt{(6)^2+(0)^2}\)
 
\(D=\sqrt{36+0}\)
 
\(D=\sqrt{36}\)
 
\(D=6\)

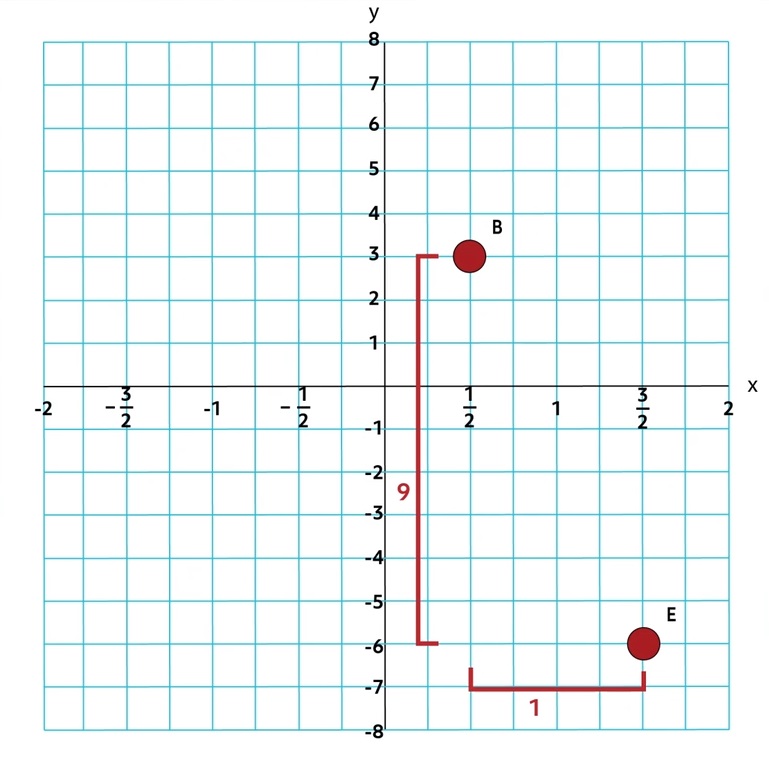
In this case, we can see that the coordinates of Point B are \((\frac{1}{2},3)\) and the coordinates of Point E are \((\frac{3}{2},-6)\). In order to determine the distance between the two points, we’ll need to use the formula because the points do not share a gridline, so we can’t simply count squares to determine the distance.

\(D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
 
\(D=\sqrt{(\frac{3}{2}-\frac{1}{2})^2+(-6-3)^2}\)
 
\(D=\sqrt{((1)^2+(-9)^2}\)
 
\(D=\sqrt{1+81}\)
 
\(D=\sqrt{82}\)
 
\(D≈9.055\)

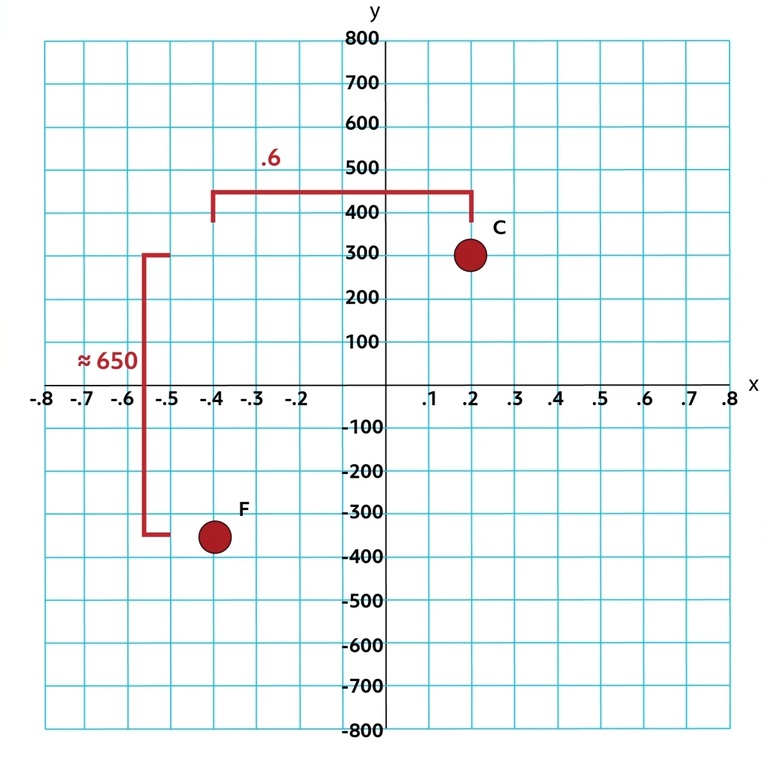
In this case, we’re going to need to estimate the coordinates of Point F because it doesn’t lie at the intersection of two gridlines. It is often the case that we need to estimate the coordinates of a point. Let’s estimate Point F to be located at \((-0.4,-350)\). Now, let’s use the distance formula to get a good idea of the distance between Points C and F:

\(D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
 
\(D=\sqrt{(-0.4-0.2)^2+(-350-300)^2}\)
 
\(D=\sqrt{(-0.6)^2+(-650)^2}\)
 
\(D=\sqrt{0.36+422,500}\)
 
\(D=\sqrt{422,500.36}\)
 
\(D≈650\)

Using the coordinates of points on a coordinate plane, we can also calculate the coordinates of a point that lies exactly halfway between two points, which is known as the midpoint.

The formula for finding the midpoint coordinates looks like this:

\(M=(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\)

In words, it’s easy to remember as “the average of the \(x\)’s, the average of the \(y\)’s.”

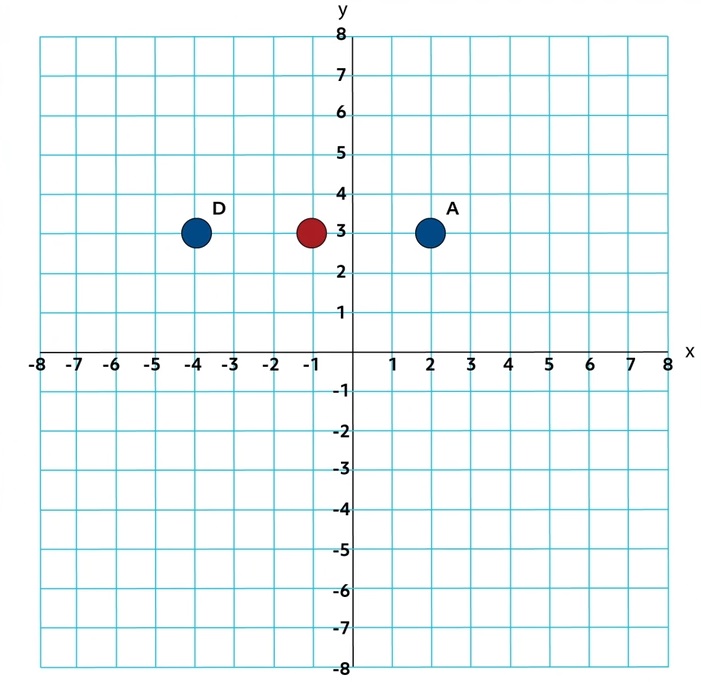
As we saw previously, the distance between Points A and D is 6. Half of that distance is 3. Since Points A and D lie on the same gridline, the midpoint will lie there as well, at the coordinates \((-1,3)\).

We can verify this with the formula:

\(M=(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\)
 
\(M=(\frac{-4+2}{2},\frac{3+3}{2})\)
 
\(M=(\frac{-2}{2},\frac{6}{2})\)
 
\(M=(-1,3)\)

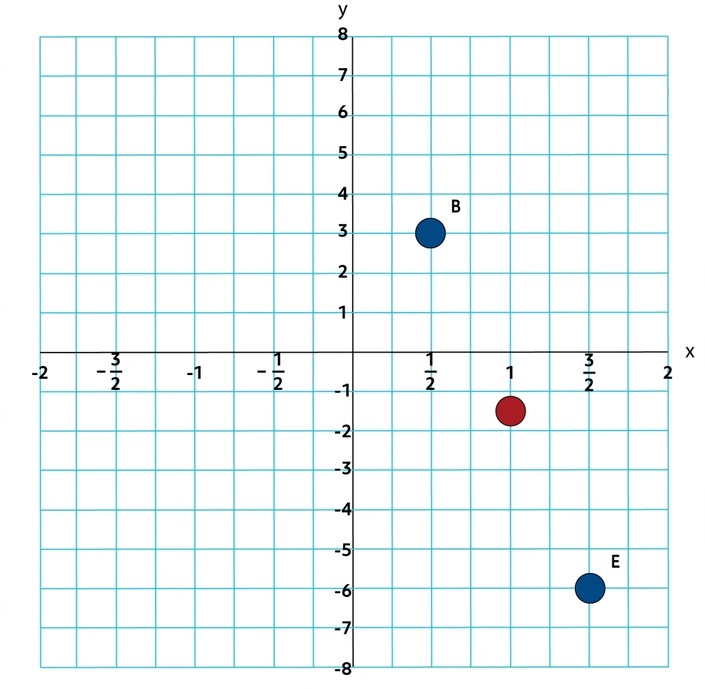
Even though we can always calculate half of the distance between two points, that won’t tell us the coordinates of the midpoint in this example like the formula does:

\(M=(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\)
 
\(M=(\frac{\frac{1}{2}+\frac{3}{2}}{2},\frac{3+(-6)}{2})\)
 
\(M=(\frac{2}{2},\frac{-3}{2})\)
 
\(M=(1,-\frac{3}{2})\)

To graph, we’ll need to estimate the location of \(-\frac{3}{2}\).

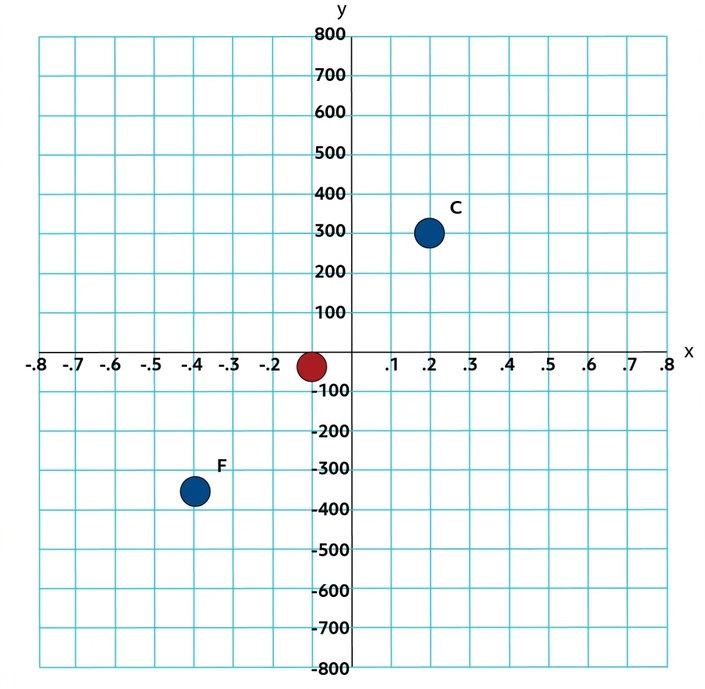
Previously, we estimated the coordinates of Point F to be \((-0.4,-350)\). Let’s use the formula to estimate the midpoint between Points C and F:

\(M=(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\)
 
\(M≈(\frac{0.2+(-0.4)}{2},\frac{-350+300}{2})\)
 
\(M≈(\frac{-0.2}{2},\frac{-50}{2})\)
 
\(M≈(-0.1,-25)\)

To graph, we’ll need to estimate the location of -25.

I hope that this video helped you understand how to perform calculations using the points on a coordinate plane! Thanks for watching, and happy studying!

Graph Practice Questions