What is Boyle’s Law?

Hi, and welcome to this video covering Boyle’s Law! In this review, we’ll be taking a look at what this law of physics is all about and discuss the relationship between temperature and pressure. We’ll go over a few practical examples along the way, so you’ll be able to understand its application in the context of many disciplines. Let’s get started!

Boyle’s Law defines the inverse relationship between pressure and volume for a collection of particles in the gas phase.

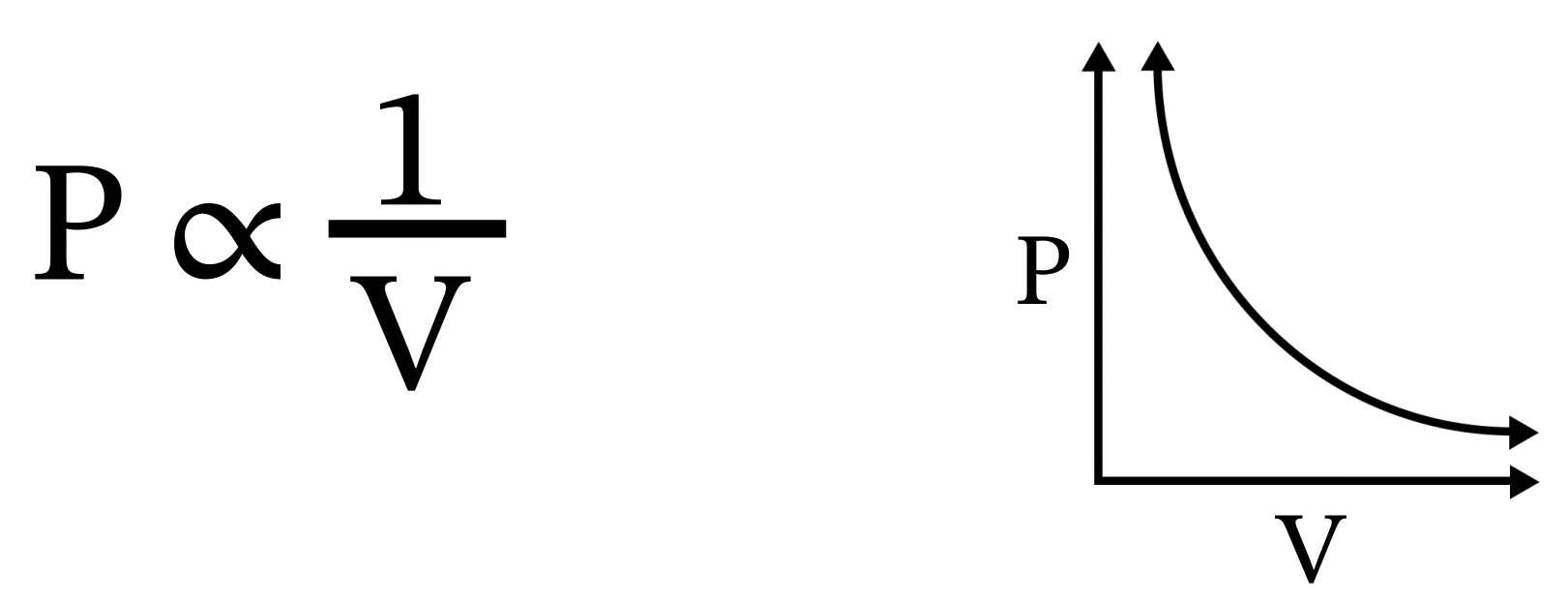
As you can see from this graph, as the volume increases, the pressure decreases.

Boyle stated that this relationship holds for a constant temperature. However, we want to put this in a simplified, more concrete context by saying that the number of gas particles (or moles of gas particles) should also be held constant.

To better interpret the mathematical nature of this statement, let’s remind ourselves what volume and pressure are.

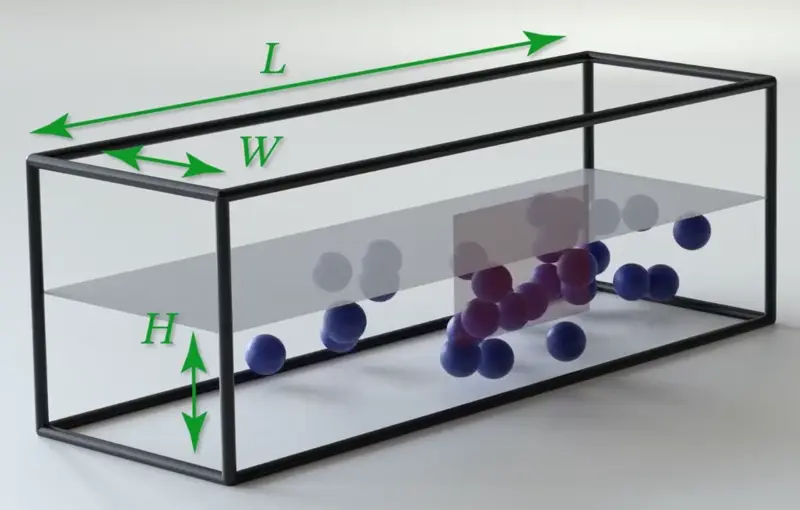
Simply put, volume is a measurement of distance in three dimensions. A rectangular box, for example, has the dimensions of length (L), width (W), and height (H). The volume of the box is \(V = L×W×H\).

Now let’s look at pressure. Pressure is defined as the force per unit area.

Imagine we have a flat surface with a certain area. This would be \(A = x^2\).

Let’s now say that this flat area has a force pressing against it. We could use our equation \(P = F/A\) to measure the pressure.

Now, imagine that area was part of the box from earlier whose volume is \(L×W×H\).

This vessel has some gas molecules in it.

Each time one of those particles collides with the wall of the vessel, it exerts a force. The amount of force per unit area is a function of the number of particles contained in that volume.

You might be able to tell by looking at this that time is also a factor, because the number of particles hitting a certain area also depends on how fast the particles are moving. As we’ll see a bit later, pressure is also a function of temperature. Boyle did his experiments with a constant temperature, so we’re going to imagine that the velocity of the particles is constant.

Now, let’s say that we could move the top of our box downward, like how a piston in a car engine works. This would reduce the volume of the vessel.

As you can see, though the particles are moving at the same speed, more particles are hitting that area more frequently, and, therefore, the pressure inside the vessel has increased. A smaller volume leads to larger pressure at constant temperature and a constant number of particles.

As we talk about Boyle’s Law, it’s important to have a qualitative understanding of the inverse nature that this law indicates. To do this, let’s put this law in the context of what is known as the ideal gas law.

In this equation, n is the number of moles, T is the temperature, and R is the ideal gas constant.

The meaning of “ideal” in the phrase “ideal gas law” implies the molecules in an ideal gas have no intermolecular interactions due to electrostatic charges or charge distributions surrounding the atoms or molecules.

The general term for intermolecular interactions is “Van der Waals forces.” Here’s a quick look at the different forces included here. There are dipole-dipole interactions, hydrogen bonding, ion-dipole interactions, and London dispersion forces:

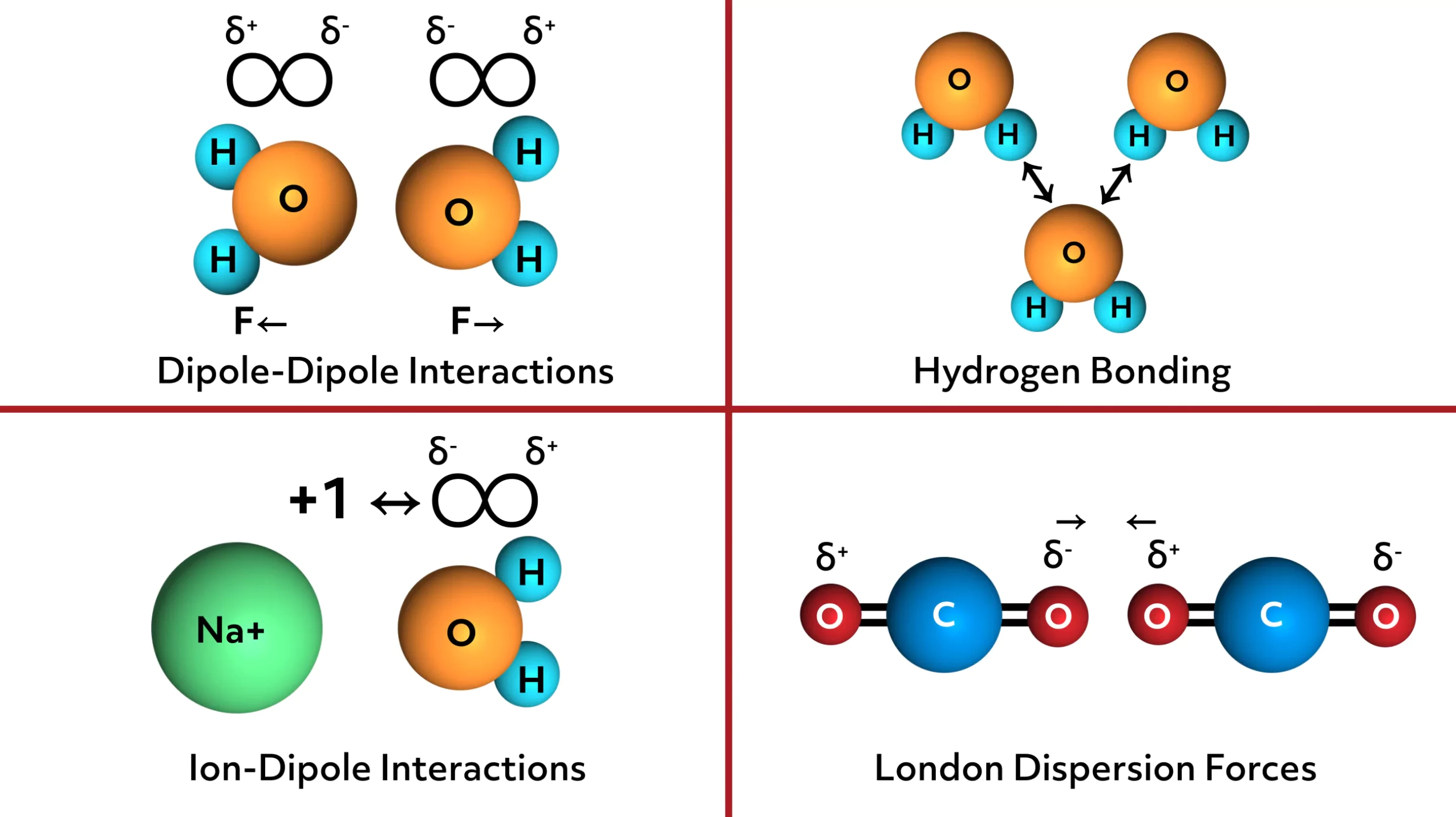
When none of these intermolecular forces are present in a collection of gas molecules, the ideal gas law accurately represents the dynamics of a collection of “n” moles of a gas at a given temperature, pressure, and volume.

Let’s consider a system under a constant temperature and look at the relationship between the pressure and the volume. We can note that assuming a constant number of particles, the equation’s right side is a constant.

So, if we look at a system with an initial P₁ and V₁ and then change the volume and note the corresponding pressure change, then we can set P₁V₁ = P₂V₂.

This is an expression of Boyle’s Law for a system with a constant temperature and number of moles of gas.

Let’s look at a couple of examples illustrating how Boyle’s Law is applied and do some simple calculations to understand the nature of the inverse relationship.

For our first example, let’s look at a piston.

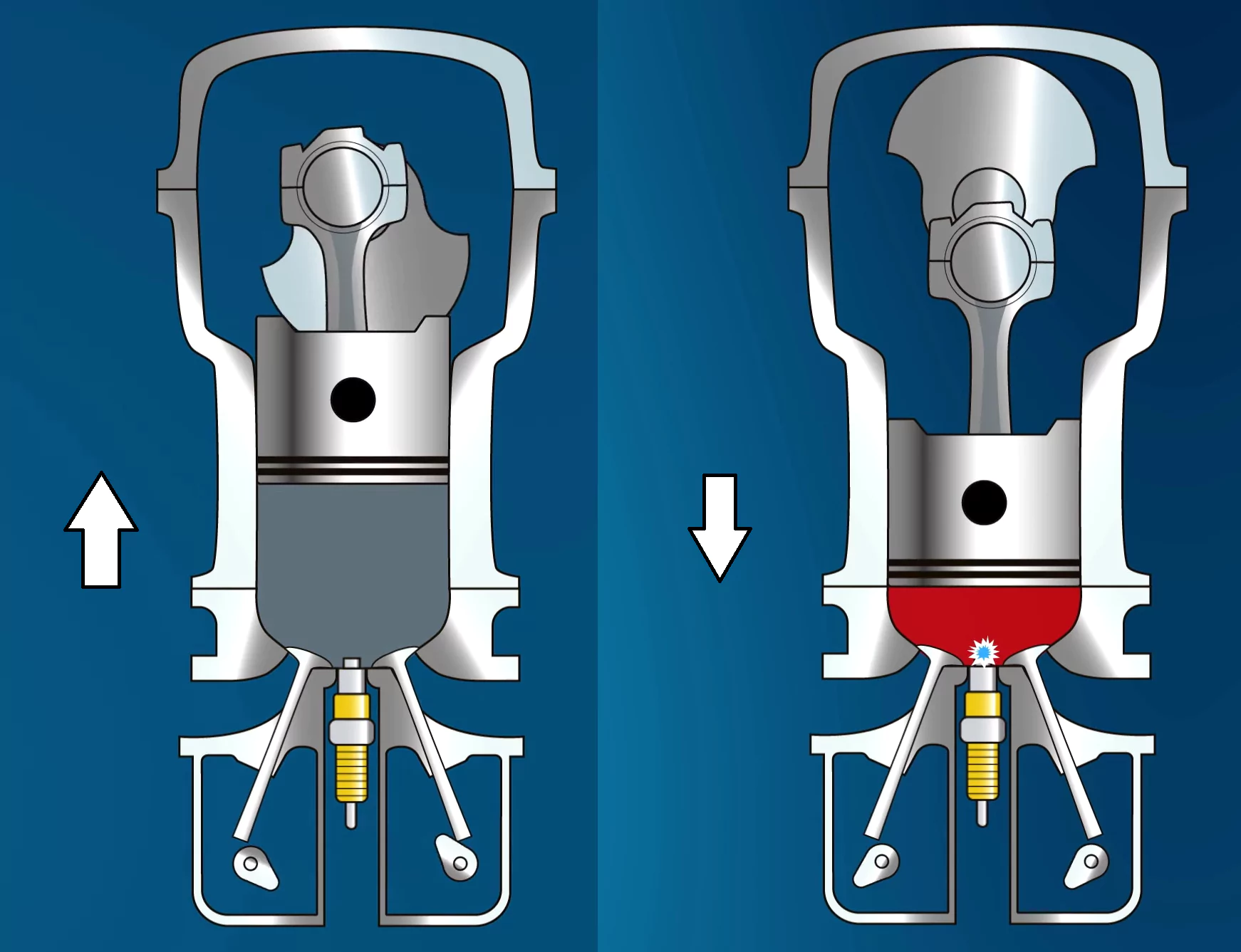
If we move the piston down inside the vessel, decreasing the volume, the pressure of the gas particles will increase. Since we are assuming the number of particles in the cylinder is constant and the temperature is constant, we can use Boyle’s Law to calculate the pressure as the volume changes, using the ideal gas law.

Let’s say that the original pressure in the cylinder was 2 atmospheres, the original volume was 3 liters, and the piston compressed the gas into a volume of 0.2 liters.

We can solve the equation for P₂ = P₁ × (V₁/V₂) by plugging in our numbers:

 
This gives us our numerical answer, which is 30 atmospheres.

 
Note that because the volume went down, the pressure went up, confirming the inverse nature that Boyle identified.

As a second example, let’s look at a zeppelin, which is a lighter-than-air vehicle.

Imagine that the zeppelin is on the ground, where the pressure is 1 atmosphere, and that we fill the zeppelin with a fixed number of moles of helium. We’ll also say that the volume of our zeppelin is 2.40×105 L.

Now, let’s say that we want to send this zeppelin into the sky to a height of 4 kilometers. At that height, the air pressure is significantly lower, measuring approximately 0.61 atmospheres.

Furthermore, if the temperature is constant, we know that the zeppelin will expand with a decrease in pressure. If the zeppelin can expand to a maximum volume of 3×105 L before bursting, will the zeppelin explode when it reaches that height?

Of course, with the given conditions, we can use Boyle’s Law to figure this out.

This time, we need to solve for V₂ = V₁ (P₁/P₂).

Then, plug in the numbers.

 
The value obtained from Boyle’s Law exceeds the maximum volume allowed, which means that the zeppelin would indeed explode.

Again, note the inverse relationship: as the pressure decreased, the volume increased.

Review

Now that we’ve looked at a couple of examples, let’s finish up with a few review questions:

1. Which of the following is Boyle’s Law related to?

1. The ideal gas law
2. The first law of thermodynamics
3. The boiling point and its relation to vapor pressure
4. The Van der Waals equation

2. Which of the following are held constant in the ideal gas law PV=nRT to show Boyle’s Law?

1. The number of moles of a gas and the pressure
2. The pressure and the temperature
3. The pressure and the number of moles
4. The temperature and the number of moles

That’s all for this review! Thanks for watching, and happy studying!