
Hello, and welcome to this video about arcs and angles of circles! In this video, we will explore the different parts of circles and how to use them to solve problems.
Let’s learn about arcs and angles of circles!
What is an Arc?
When we look around us, after polygons, circles are the next most common shape that we are surrounded by in our environment. A circle is created by a 360° rotation.
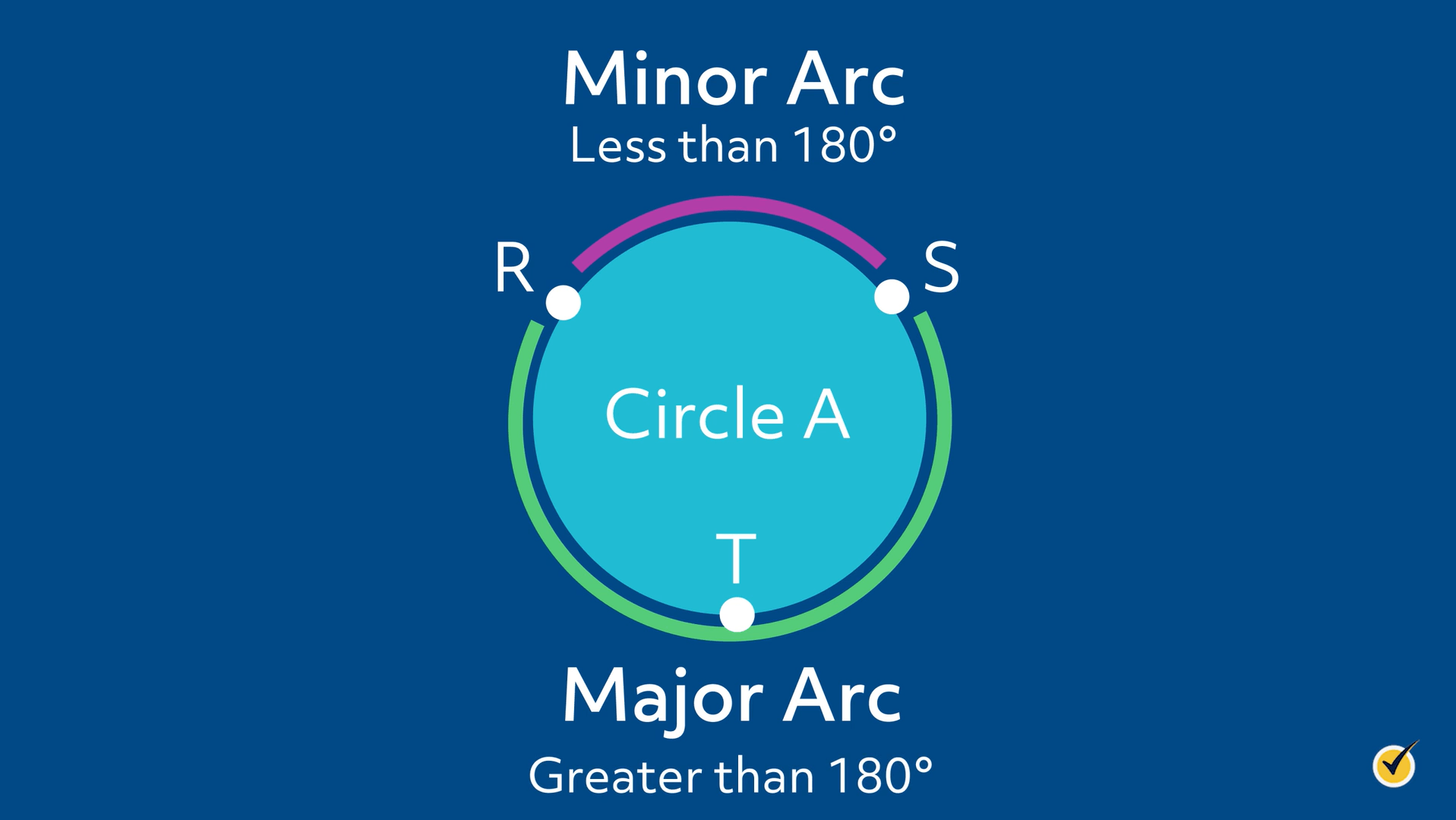
An arc of the circle is a part of the circle, and we identify arcs using points on the circle.
Arc \(RS\) is the curved part of circle \(A\) shown with the purple mark. Because arc \(RS\) is less than 180°, we call this arc a minor arc. Arc \(RTS\), or \(STR\), is a major arc because it is greater than 180°.
Finding the Measure of an Arc
We can find the measure of an arc using the fact that a circle is 360°. If we know that the measure of arc \(RS\) is 130°, we can find the measure of arc \(RTS\) by subtracting the measure of arc \(RS\) from 360°, which would make the measure of arc \(RTS\) 230°.
Some important lines and segments associated with circles are chords, secants, and tangents.

Chords, Secants, and Tangents
A chord is a line segment with either end touching the circle. Line segment \(LM\) is a chord on circle \(A\).
A secant line is similar to a chord, except it is a line that passes through two points on the circle instead of being a line segment.
And a tangent line is a very special kind of line that only touches the circle at one point, called the point of tangency. Line \(PQ\) is a tangent and point \(Q\) is the point of tangency.
Knowing these vocabulary words related to circles is important in helping understand the circle theorems which will help us solve problems.
The radius of the circle is always perpendicular to the point of tangency.
Inscribed Angle Theorem
When two chords share a point on the circle, an inscribed angle is formed. In circle \(A\), the chords \(RS\) and \(TS\) form the inscribed angle \(RST\), which has its vertex on the circle.
The arc that is formed by the legs of angle \(RST\) is called an intercepted arc.
An angle that has the center of the circle as its vertex is naturally called a central angle. In circle \(C\), angle \(MCN\) is a central angle and arc \(MN\) is its intercepted arc.
If we are given the measure of the inscribed angle or the intercepted arc, we will be able to find the measure of the other using a circle theorem that tells us that the measure of an inscribed angle is one-half the measure of its intercepted arc. Or we could say that the intercepted arc is twice as long as the inscribed angle.
For example, in circle \(A\), the measure of inscribed angle \(RST\) is given to us as 60°. According to the inscribed angle theorem, the measure of arc \(RT\) is \(60° \times 2\), which is 120°.
Here is a special case of an inscribed angle.
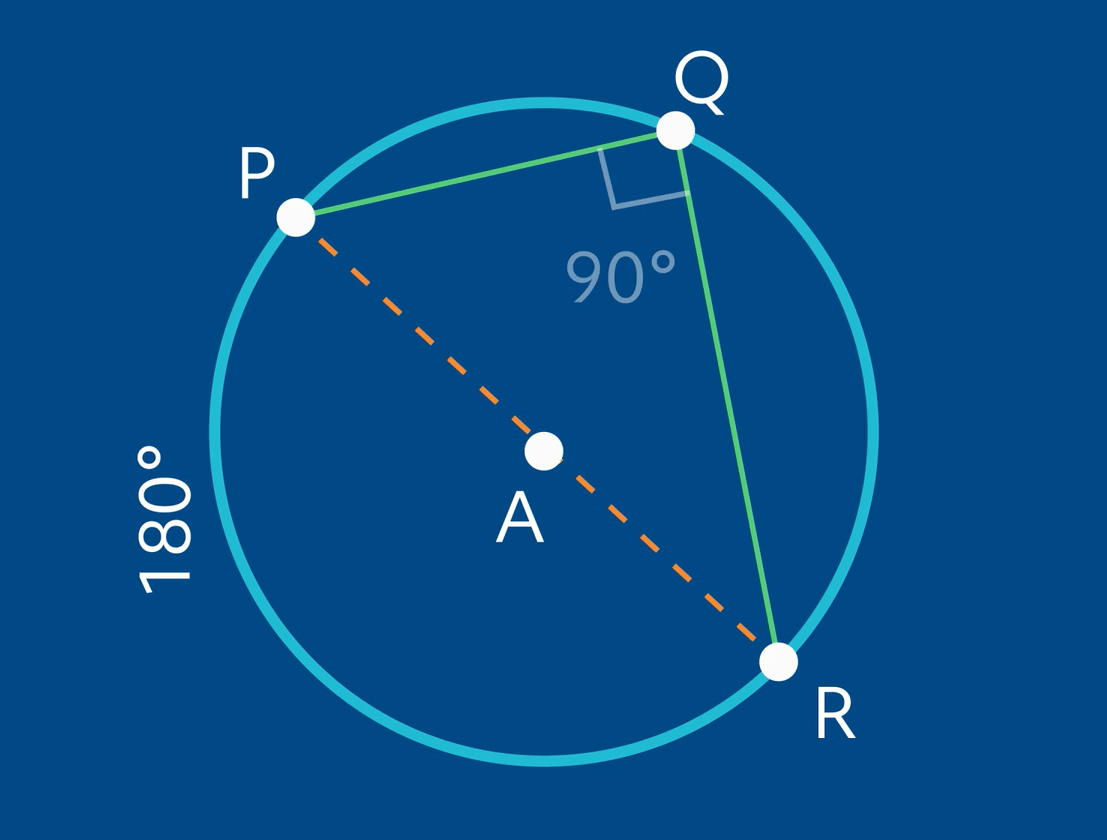
In circle \(A\), inscribed angle \(PQR\) encompasses the diameter of the circle, line segment \(PR\) Remember, the diameter of the circle divides the circle into two equal parts, called semicircles.
A circle has a total of 360°, so a semicircle has 180°, or half the measure of a full circle. So this must mean that the intercepted arc of angle \(PQR\) is 180°. If we use the inscribed angle theorem, we find out that angle \(PQR\) is 90° because it is half the degree measure of the intercepted arc.
Central Angle Theorem
Another important theorem we are going to take a look at is the central angle theorem. This theorem says that the measure of a central angle is equal to the measure of its intercepted arc. In circle \(C\), since the measure of angle \(MCN\), the central angle, is 110°, then arc \(MN\), its intercepted arc, is also 110°.
Let’s take a look at an example problem. Line \(LM\) is tangent to circle \(T\) at point \(L\). The measure of the central angle \(T\) is 35°. What is the measure of angle \(LMT\)?
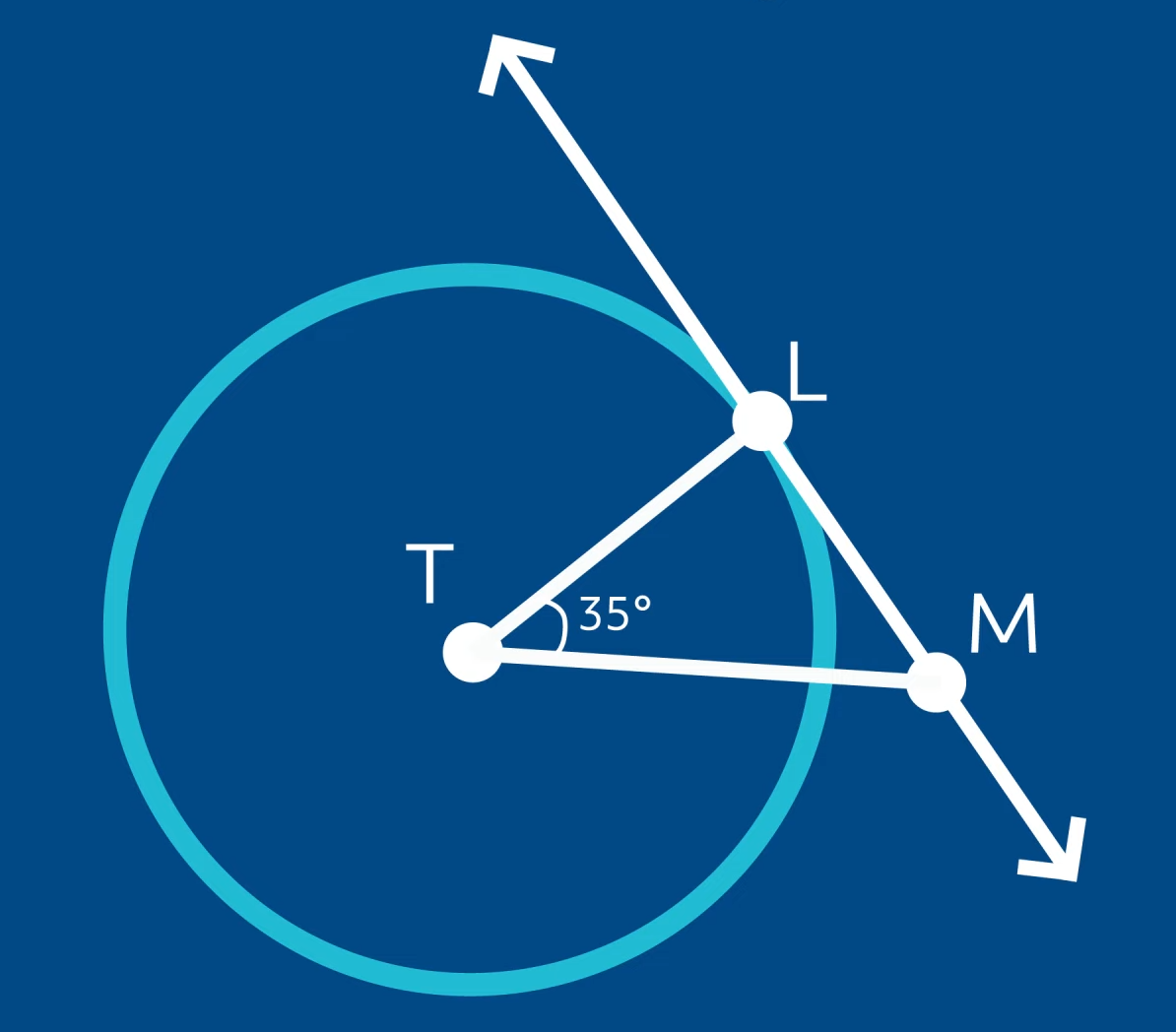
Since we know that the sum of the interior angles of any triangle is 180° and that the radius is always perpendicular to the point of tangency, we know that angle \(TLM\) is 90°. We can subtract \((90°+35°)\) from 180° to find the measure of angle \(LMT\). \(180 – (90+35) = 55\), therefore the measure of angle \(LMT\) is 55°.
When secants intersect inside a circle, we can find the measure of the vertical angles created by using the measure of the arcs formed by the angles. It also works the other way around, if we need to find the measure of the arcs using the measure of the angles.
Let’s take a look at circle \(K\).
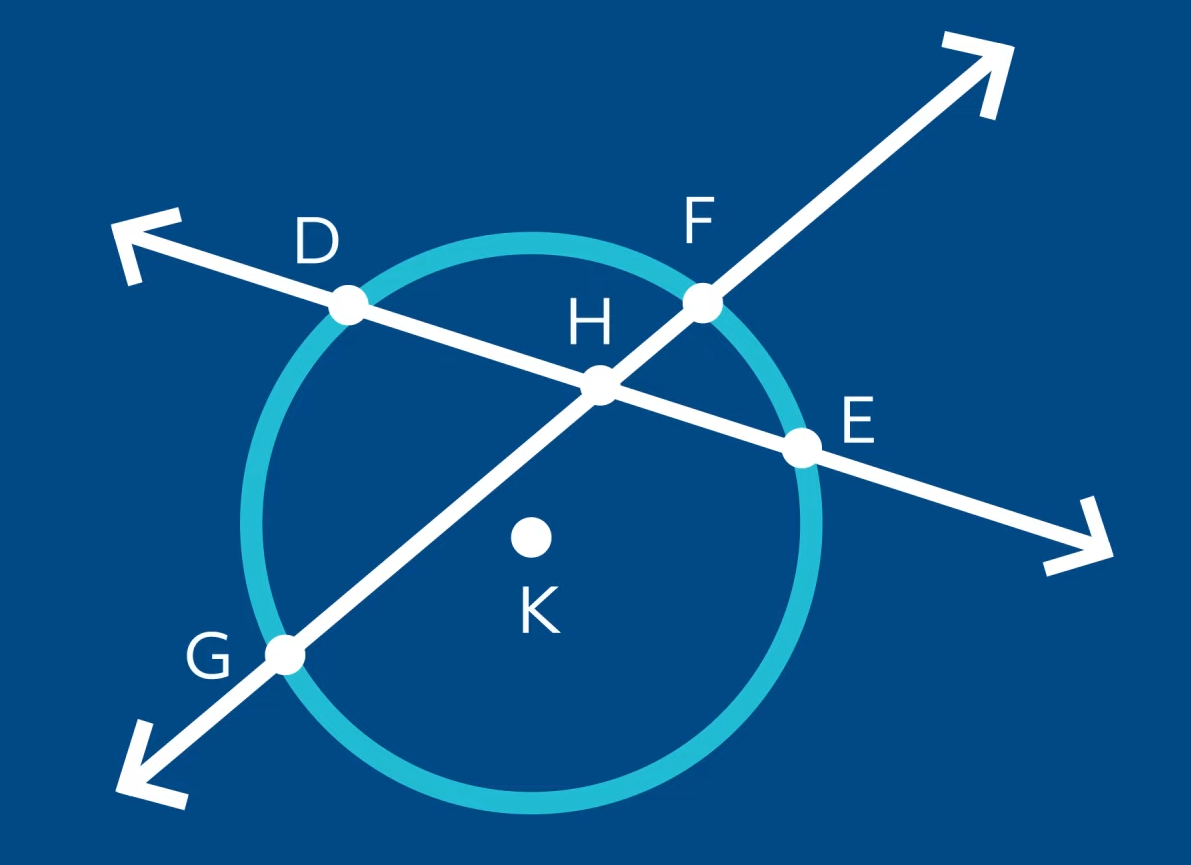
The secant lines \(DE\) and \(FG\) intersect at point \(H\) and create the arcs \(DF\), \(FE\), \(EG\), and \(GD\). Find the measure of any of the vertical angles (notice that there are two sets) by adding together the measures of the intercepted arcs and dividing by 2.
We will use the formulas \(m\angle DHF=\frac{1}{2}\) (arc \(DF\) + arc \(GE\)) and \(m\angle FHE=\frac{1}{2}\) (arc \(FE\) + arc \(DG\)). Then we will use the vertical rule theorem to find \(m\angle EHG\) and \(m\angle GHD\).
Let’s practice. The measure of arc \(GE\) is 170°, arc \(GD\) is 80°, arc \(DF\) is 60°, and arc \(FE\) is 50°. To find the \(m\angle DHF\), we will add the intercepted arcs, \(DF\) and \(GE\), then multiply by \(\frac{1}{2}\). Therefore, \(m\angle DHF=\frac{1}{2}(60° +170 °)\). So \(\angle DHF=115° \). We will use the equation, \(m\angle FHE=\frac{1}{2}(50° +80°)\) to find the measure of \(\angle FHE\), which is \(m\angle FHE=65°\).
When two secant lines intersect outside the circle, we use a different method to find the measure of the angles. When this happens, you look at the two intercepted arcs created by the angle and subtract the measure of the smaller arc from the measure of the larger arc, then multiply by \(\frac{1}{2}\).
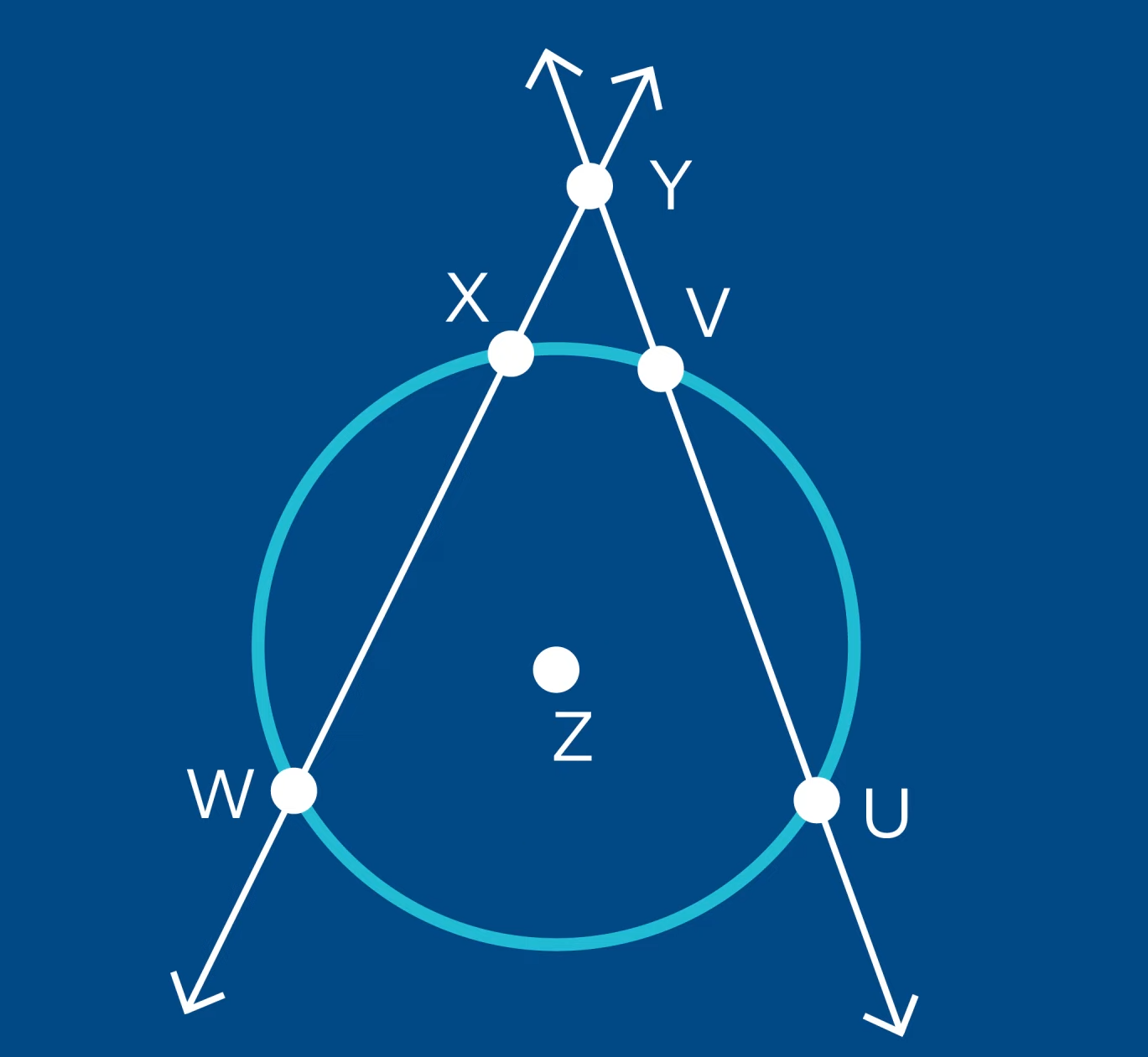
We want to find the \(m\angle WYU\) that is created by the intersection of secants \(WX\) and \(UV\) on circle \(Z\). \(\angle WYU\) is intercepted by arcs \(XV\) and \(WU\). The measure of arc \(XV\) is 30°; the measure of arc \(WU\) is 80°. To find the measure of angle \(WYU\), we use the formula: \(m\angle WYU= \frac{1}{2}\) (arc \(WU\) – arc \(XV\)), therefore, \(m\angle WYU=\frac{1}{2}(80°-30°) \text{, }m\angle WYU=25°\).
A sector of a circle is a section of a circle between two radii. The red area in the diagram is an example of a sector.
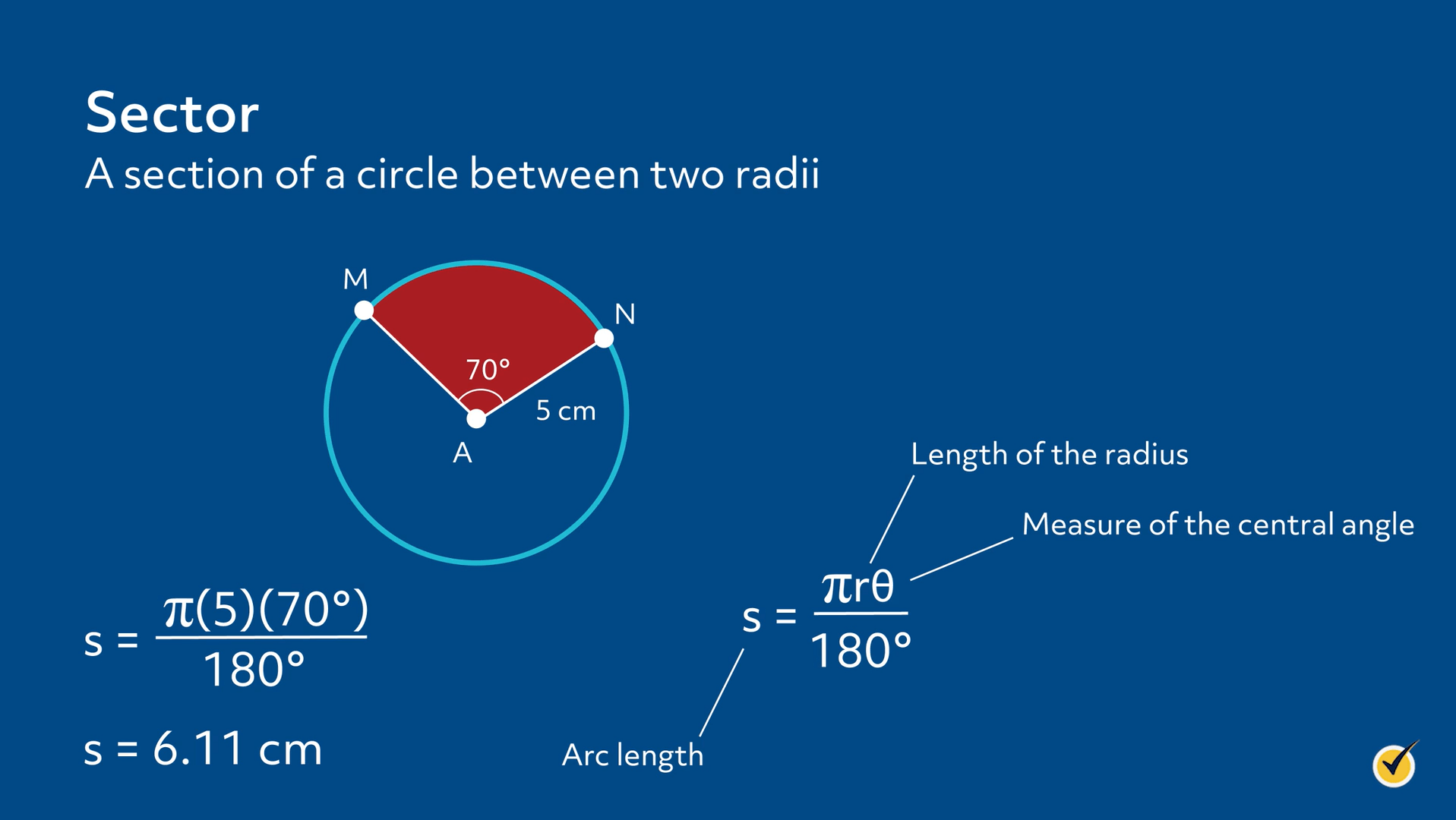
We can find the length of an arc if we are given the length of the radius and the measure of the central angle using the formula \(s=\frac{\pi r\theta }{180°}\), where \(s\) is the arc length, \(r\) is the length of the radius and \(\theta \) is the measure of the central angle. In circle A, the length of the radius is 5 cm, and the measure of angle \(MAN\) is 70°. We want to find the length of arc \(MN\). We will start by substituting what we have into the formula, \(s=\frac{\pi (5)(70)}{180°}\). We will simplify to get \(s=6.11\text{ cm}\) , which is the length of arc \(MN\).
Thanks for watching this video, and happy studying!
Arcs and Angles of Circles Practice Questions
If angle \(B\) is \(21°\), what is the measure of arc \(AC\)?
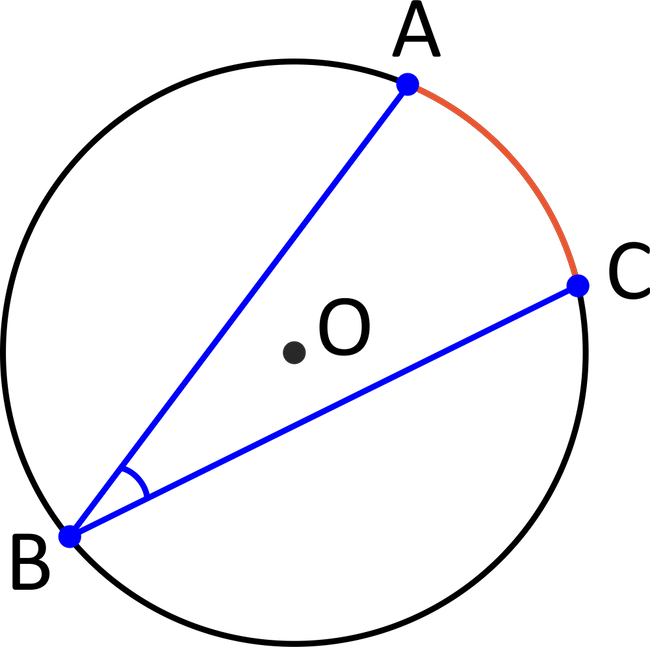
According to the inscribed angle theorem, arc \(AC\) will be twice as large as the inscribed angle \(B\). This means that arc \(AC\) will be \(2×21°=42°\).
Line \(LM\) is tangent to circle \(J\) at point \(L\). If angle \(J\) is \(27°\), what is the measure of angle \(M\)?
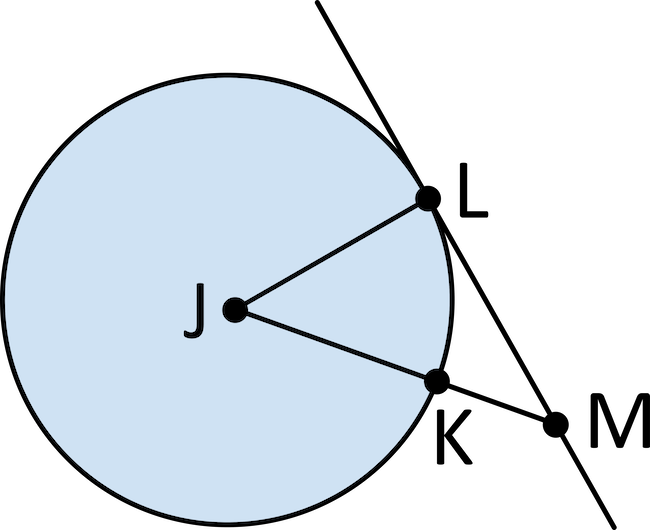
Since line \(LM\) is tangent to circle \(J\) at point \(L\), the line \(JL\) and \(LM\) form a right angle. This means that angle \(L\) is \(90°\). Angle \(J\) is \(27°\), so add angle \(J\) and angle \(L\): \(90+27=117\). Since there are \(180°\) in a triangle, subtract \(117\) from \(180\): \(180-117=63\). The measure of angle \(M\) is \(63°\).
Arc \(BD\) is \(15°\). Arc \(AE\) is \(48°\). Find the measure of angle \(ACE\).
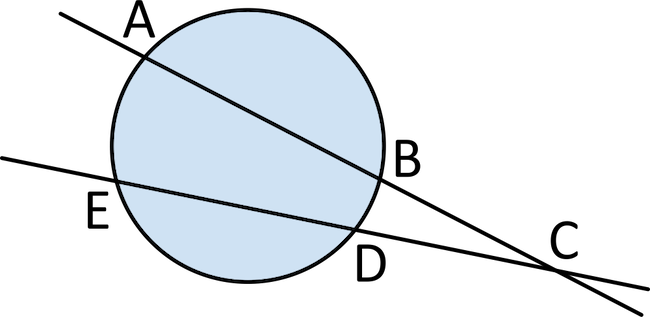
Look at the two intercepted arcs. The angle \(ACE\) will be \(\frac{1}{2}\) the difference between the arc lengths of these intercepted arcs. Subtract the smaller arc from the larger arc. In this case, subtract arc \(BD\) from arc \(AE\): \(48-15=33\). Now multiply this by \(\frac{1}{2}\). \(33×\frac{1}{2}=16.5°\). Angle \(ACE\) is \(16.5°\).
You are walking around a circular pond from one star to the other. If the radius of the pond is \(8\text{ ft}\), what distance have you walked? Use \(3.14\) for \(π\).

Find the measure of the arc by using the formula: \(s=\frac{πrϴ}{180°}\)
\(s\) represents the arc length.
\(π\) is approximated to \(3.14\).
\(r\) is the radius.
\(ϴ\) is the central angle measure.
\(s=\frac{πrϴ}{180°}\) becomes \(s=\frac{(3.14)(8)(120°)}{180°}=16.746\), which simplifies to \(s=16.7\text{ ft}\).
A flashlight shines across a circular field. What is the angle measure of the intercepted arc that will be illuminated?
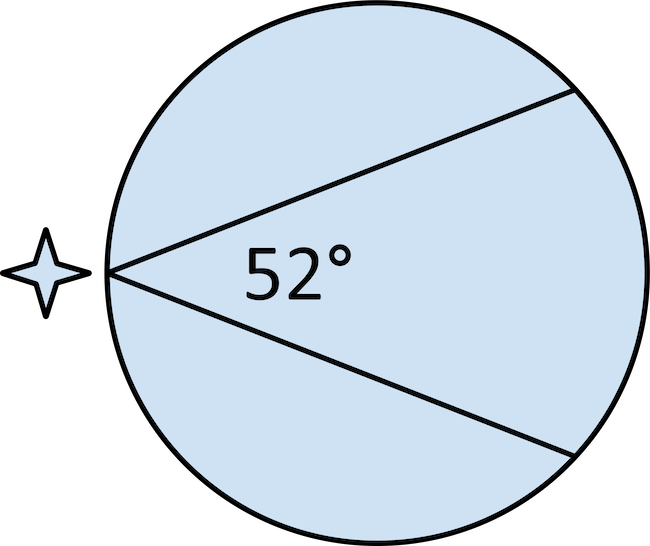
The inscribed angle is \(52°\). The intercepted arc will be twice as much as the inscribed angle. \(52×2=104\). The angle measure that is illuminated across the field is \(104°\).