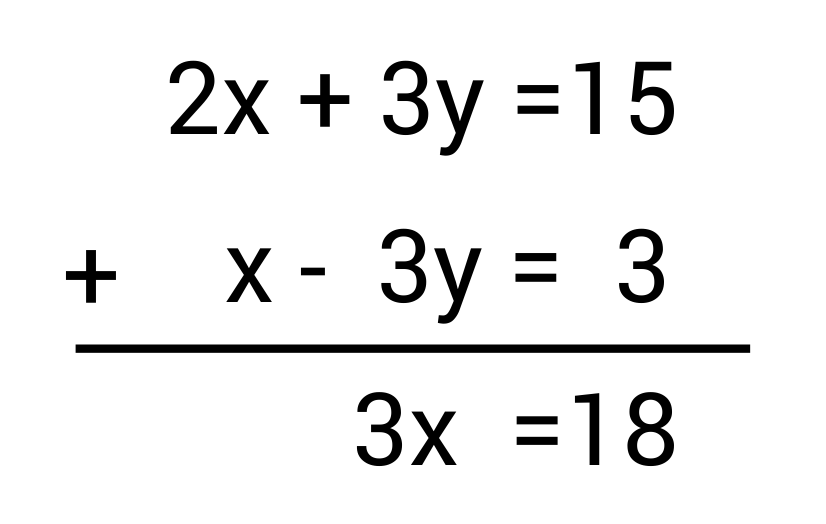Hey, guys! Welcome to this video over comparing different methods for solving a system of equations.
If you recall, a system of equations is when you have more than one equation with unknown variables in a given problem. So, in order to solve that problem, you need to be able to find the value of all the variables in each equation.
Substitution, Elimination, and Augmented Matrix
There are three different ways that you could do this: the substitution method, elimination method, and using an augmented matrix.
In this video, I’m assuming that you already know how to perform each method, so I want to spend a lot of time explaining not how to do them but rather when to use each method.
First, I will verbally tell you when to use each method, then I will write out three different examples, and we will decide together which method is most efficient for each system.
When to Use the Substitution Method
You should use the substitution method when one of the variables in one of your equations has already been isolated (it has a coefficient of 1).
When to Use the Elimination Method
You should use the elimination method when the same variables in all of the equations share the same coefficient, or when they share the same but negative coefficient.
When to Use an Augmented Matrix
You would use an augmented matrix when the substitution and elimination method are either impractical or impossible altogether.
Now, let’s look at three different systems, and use what we’ve just learned to think through which method is most useful for each system.
So, what we will do is go through each system, decide which method would be most efficient, and then solve with that method.
Elimination Method Example
Alright, let’s look at this first equation.
Now, thinking back to the explanation I gave on when to use each method, notice what I said about elimination: “You should use the elimination method when the same variables in all of the equations share the same coefficient, or when they share the same but negative coefficient.”
Well this exact thing is true in the case of this particular system. So, let’s solve this system using elimination.
Now, we plug our
Great, so we’ve solved this system using elimination, because our same two variables had the same coefficient or when they share the same but negative coefficient (like in our case).
Substitution Method Example
Let’s move on to system #2.
Alright, so again, let’s think back on what was said in our explanation on when to use each method. Recall what was said about substitution: “You should use the substitution method when one of the variables in one of your equations has already been isolated.”
Well, such is the case with this system. Our
That was very simple to solve using substitution. Remember, the signifier to help you know when to use it is if one of the equations has a variable that is already isolated.
Augmented Matrix Example
Let’s look at our last system, system #3.
Remember, what we said about when to use an augmented matrix. Well, right now is a good time. Using elimination or substitution for that matter would take a lot more work than would using an augmented matrix.
So, let’s set up our matrix and solve.
I hope that this video over the comparison of methods for solving systems was helpful for you.
See you guys next time!
Frequently Asked Questions
Q
What is a system of equations?
A
Systems of equations are two or more equations that can be used to solve one another.
Ex.
Q
How do you do the substitution method?
A
The substitution method of solving linear equations involves substituting one equation for a variable in the other equation, solving for one of the variables, and then using that variable and one of the original equations to solve for the other variable.
Ex. Solve: 2x + 3y = 15 and y = 2x + 1
Substitute 2x + 1 for y
2x + 3(2x + 1) = 15
Solve for x
2x + 3(2x + 1) = 15
2x + 6x + 3 = 15
8x + 3 = 15
8x = 12
x = 3
Solve for y by substituting 3 for x in either original equation
y = 2(3) + 1 = 6 + 1 = 7
The solution to these two equations is the point (3, 7).
Q
How do you do the elimination method?
A
To use the elimination method of solving systems of equations, manipulate one of the equations so it can be added to, or subtracted from, the other equation where one variable will cancel out. Then, solve for the other variable. Finally, use that variable to solve for the one that originally was eliminated.
Ex. Solve:
Then, add the two equations.
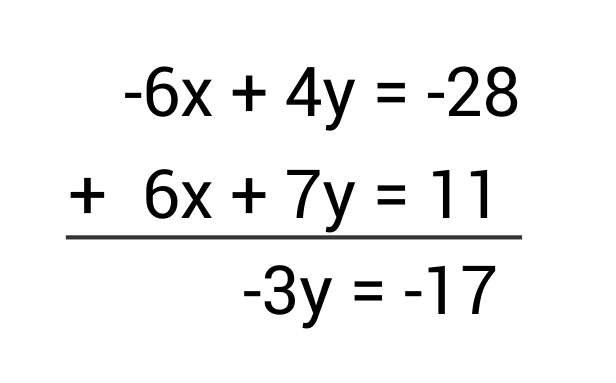
Solve for y by dividing by -3 on both sides.
Then, substitute y in either original equation to solve for x.
The solution to this system is the point (
Q
What is an augmented matrix?
A
An augmented matrix is formed by appending the entries from one matrix onto the end of another.
Ex.
Systems of Equations Practice Questions
Solve the system of equations by substitution:
Solve the system of equations using substitution.
Solve the system of equations by elimination:
The admission fee at an amusement park is $2.50 for children and $4.50 for adults. On Monday 2,000 people entered the amusement park and $8,000 was collected. How many children and how many adults went to the amusement park on Monday?
A potter is selling bowls and cups at an art fair. This morning he sold 30 bowls and 4 cups and made a total of $1,040. Later in the afternoon he sold 8 bowls for a total of $256. Find the price per bowl and cup.