Expected Value
Hello and welcome to this video about expected value! In this video, we will explore what expected value is and how it can be used.
Expected value is an application of probability that is typically used to help people make decisions about the viability of risks, most often financial risks. The big idea is to multiply the probability of each potential outcome of an event by the value of that outcome and add all the results together in order to make a more informed decision.
Let’s begin by talking about coins. The probability of flipping a coin and it landing on heads is 1 out of 2, as is the probability of landing on tails. Let’s say that you are thinking about playing a game that costs $1.00 to enter. The game will pay you $2.00 if the coin lands on heads and $0.00 if the coin lands on tails. Let’s make a table. Here we have heads and tails and on the left we have the value of the outcome and the probability of the outcome. If you win the game, you get $2.00, but since you pay $1.00 to play in the first place, we subtract that from the $2.00, which gives us $1.00. This means that if the coin lands on heads, you are one dollar richer than before you played. Now, if the coin lands on tails, you win no money and we still have to subtract that one dollar we spent to play the game, so we come away with one less dollar than we started out with. And like we mentioned before, a coin has two sides, so the probability of the outcome in both cases is 1 out of 2.
To calculate the expected value, we’ll use this formula: \(E(x)=x_1p_1+x_2p_2\)
If we plug in our numbers, our calculation looks like this:
\(E(x)=(\frac{1}{2})(1)+(\frac{1}{2})(-1)=$0.00\)
An expected value of $0.00 illustrates that the probabilities of the event outcomes and the values of those outcomes are equal, as is shown in the table. The game is balanced.
You decide not to try the coin game another time and instead head over to the movie theater. On the concession counter is a drawing that costs $1.00 to enter. The first entry drawn wins 2 movie tickets (a $30.00 value), the second entry drawn wins a large popcorn and drink (a $15.00 value) and the third ticket drawn wins a large popcorn (an $8.00 value). You ask the manager how many entries they tend to get for drawings and he says about 100. Do you take the chance? Let’s fill in our table, looking at each prize individually:
You know that drawings are stacked against you in the first place, but since the expected value shows a loss that is less than half of your cost to enter, the risk is acceptable. You decide to take the plunge.
After the movie you head home. You check your mail and find an ad for bundling TV, phone, and internet in one package using a service that isn’t even available in your area. The ad is elaborate, high-quality, and beautifully printed on glossy cardstock. You wonder how the company makes any money sending these costly ads to places that can’t even take advantage of them.
The company knows that they’ll get about a 1% return on their mail investment. In other words, they’ll get one long-term customer for every one hundred ads that are sent. If a long-term customer is worth at least $3600 and each ad costs $5.00 to print and mail, is sending direct mail a profitable idea for the company if they send 10,000 ads?
On average, the company can expect to gain $31.00 for each ad that is sent, which is a very lucrative decision!
You throw the ad in the trash and begin looking forward to the outdoor festival you are planning to attend the next day. You check to see what the weather will be like and discover a 75% chance of rain. You remember an article you read describing how $25,000 was spent by the city to put the festival together. Tickets cost $10.00 apiece and the expected turnout is about 8500 people. Is it still a good idea to put on the festival, given the rain chances? Let’s map it out and see:
\(E(x)=(.25)(60,000)+(.75)(-25,000)=-$3,750\)
With these rain chances, the expected value of the city’s investment is -$3750. They may want to postpone the festival for a sunnier day.
Thanks for watching this overview of expected value! I’ll see you next time.
Expected Value Practice Questions
What is the correct formula for expected value?
Expected value is calculated by multiplying all of the possible outcomes by the likelihood each outcome will occur, then adding all of these values.
Your friend wants you to join him in a business endeavor. He says that both of you are likely to make a lot of money in the process, so you listen to his offer. Your friend recommends two options. Project A has a 20% chance of producing a $2,500,000 profit, and a 80% chance of producing a $400,000 profit. Project B has a 35% chance of producing a $3,350,000 profit, and a 65% chance of producing a $200,500 profit. Which project sounds like the more lucrative option? Use the expected value formula to determine the best choice.
The expected value of Project A is greater.
The expected value of Project B is greater.
The expected value of Projects A and B are the same.
Project A: \(E(X)=(0.2\times2{,}500{,}000)+(0.8\times400{,}000)\)
The expected value of Project A is $820,000.
Project B: \(E(X)=(0.35\times3{,}350{,}000)+(0.65\times200{,}500)\)
The expected value of Project B is $1,302,825.
Project B would be the more lucrative business endeavor because it has a larger expected value.
Michael is playing games at a carnival with some of his friends. One of the games is a dice game. Michael isn’t sure if he should pay money to try the game. It costs $10 each time you play, but there are a few tempting cash prizes so he is considering it.
The rules of the game:
($10 to play each round)
| Number Rolled | Cash Prize |
| 1 | $0 |
| 2 | $0 |
| 3 | $0 |
| 4 | $0 |
| 5 | $20 (Remember to deduct $10 from this.) |
| 6 | $30 (Remember to deduct $10 from this.) |
Would you advise Michael to play the dice game, or walk away? Use the expected value formula to support your claim.
Play the game! The expected value is +$1.67.
Walk away! The expected value is -$1.67.
\(E(X)=(\frac{1}{6}\times-10)+(\frac{1}{6}\times-10)+(\frac{1}{6}\times -10)+(\frac{1}{6}\times-10)+(\frac{1}{6}\times10)+(\frac{1}{6}\times20)\)
\(E(X)=-1.67\) when the equation is simplified.
The negative expected value tells us that the game is not balanced, so Michael should walk away. If the game had an expected value of zero or a positive value, then Michael would have a good chance of making money over time. This particular dice game is designed to make money for the game operator over time, not the player.
Fernando is trying to design a coin flipping game that is fair and balanced. He decided to charge participants $2 to play the game. If heads is flipped, the participant wins $4, and if tails is flipped, the participant wins 25 cents. Has Fernando designed a balanced coin flipping game? Use the expected value formula to support your answer.
The game is balanced. The expected value is zero.
The game is not balanced. The expected value is positive.
The game is not balanced. The expected value is negative.
We can plug in each probability, along with its outcome, into the formula \(E(X)=x_1p_1+x_2p_2+…\)
*Remember to deduct the initial $2 that it costs to play the game.
The formula becomes \(E(X)=(\frac{1}{2}\times2)+(\frac{1}{2}-1.75)\).
The expected value simplifies to \(E(X)=0.125\).
If the expected value is zero, then the game is considered balanced. The game Fernando has designed is not balanced. In fact, the positive expected value indicates that the game leans slightly in the participant’s favor.
Susan is considering playing the spinner game shown below. It will cost Susan $1 each time she plays, and her prize money is shown in each section of the spinner. Susan wants to determine if it is a good idea to try the game, so she wants to determine how much money she can expect to win or lose over time.
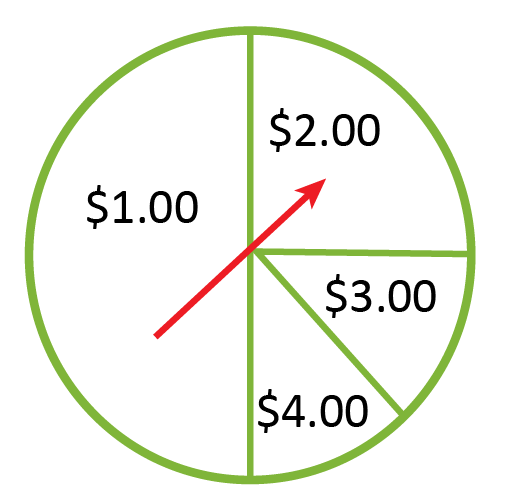
Is it a good idea for Susan to play the spinner game? Use the expected value formula to inform your decision.
Yes, Susan should try the spinner game.
No, Susan should not try the spinner game.
The probability and outcome of each section can be plugged into the expected value formula in order to determine if this spinner game is worth playing. When the values are plugged in, \(E(X)=x_1p1+x_2p_2+…\) becomes:
\(E(X)=(\frac{1}{2}\times0)+(\frac{1}{4}\times1)+(\frac{1}{8}\times2)+(\frac{1}{8}\times3)\)
This simplifies to \(E(X)=0.875\).
The expected value of this spinner game is positive, which indicates that over time, Susan will gain money and not lose money. Susan should feel comfortable about trying this spinner game because overall the expected value leans in favor of the participant.
