Rounding and Estimation

Hello! In this video you’ll learn what rounding and estimation are, how to do each of them, and see some first hand examples. Let’s get started!

Rounding and estimation both involve using approximations to simplify messy mathematics. They differ, however, in that rounding simplifies a messy number, while estimation simplifies a messy calculation.

For instance, suppose you buy a new riding lawn mower for exactly $3,184.29, but you tell your neighbor that it cost about $3,000. You have rounded the messier $3,184.29 to the simpler $3,000. On the other hand, suppose you need to buy 5 of these mowers for your lawn care business. To find the exact cost requires you to make the messy calculation 5×$3,184.29, but you can get a rough idea of the cost by instead using the estimate 5×$3,000=$15,000.

How to Round Numbers

So, how do we round a messy number? The basic plan is to replace the messy number with a nearby number that is easier to remember and easier to use in calculations. Here are the details.

When we write a number in our place-value number system, digits to the left are typically considered more significant than those to the right. To round a number, we first decide the last place—the least significant place—that we want to keep. We call this the rounding place, indicated by R. Every digit to the left of the rounding place is more significant (indicated by M) so we keep it. The next digit to the right (indicated by N) and all the remaining digits to the right are less significant (indicated by L), so we zero them out.

We must decide if we keep the digit in the rounding place (R) the same or increase it by 1. This will depend on the digit located one place to the right (N). If the next digit is 0 through 4, we keep the rounding digit unchanged. We call this rounding down.

If the next digit is 5 through 9, we increase the rounding digit by 1. We call this rounding up.

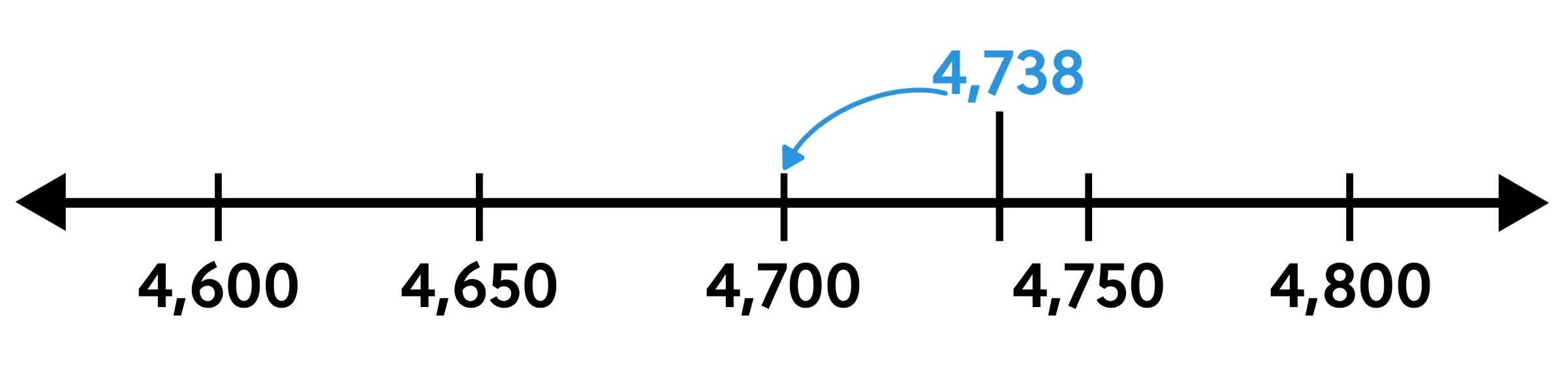
For example, suppose we want to round the number 4,738 to the hundreds place—we call this rounding to the nearest hundred. This means the 7 is in the rounding place because it is in the hundreds place. We keep the 4 because it is more significant. To decide what to do with the rounding digit, 7, itself, we look at the next digit, the 3. Since 3 is less than 5, we keep 7 unchanged. We zero out the 3 and 8 because they are less significant. So, 4,738 is rounded down to the nearest hundred giving us 4,700.

Now, suppose we want to round the number 4,738 to the thousands place—we call this rounding to the nearest thousand. This means the 4 is now in the rounding place. There are no more significant places, so we move on to deciding what to do with the rounding digit, 4. We look at the next digit, the 7. Since 7 is greater than or equal to 5, we round the 4 up by increasing it to 5. Then we zero out the 7, 3, and 8 because they are less significant. So, rounding 4,738 to the nearest thousand gives us 5,000.

Let’s put the previous examples on number lines, to help us visualize how rounding works. We rounded 4,738 to the nearest hundred, and got 4,700. If we plot 4,738 on a number line marked off by hundreds, 4,738 is closer to 4,700 than it is to 4,800.

In the next example, when we rounded 4,738 to the nearest thousand, we got 5,000. If we plot 4,738 on a number line marked off by thousands, we see that 4,738 is closer to 5,000 than 4,000.

By the way, if we ever want to round a number that is exactly halfway between two numbers on the number line, by convention we round up. This is the reason we round the rounding digit up whenever the next digit is 5.
What happens if we want to round a number to a fractional place—that is, to a place to the right of the decimal point? It turns out that the rules are exactly the same.

For instance, suppose we want to round the number 92.67381 to the nearest thousandth. Our rounding digit is the 3 in the thousandths place. We keep all the digits to the left of 3. Since the next digit, 8, is 5 or greater, we round the rounding digit up to 4. The numbers after 4 become 0. This gives us a rounded answer of 92.67400, which we can write as 92.674. This is sometimes called “rounding to three decimal places” instead of “rounding to the nearest thousandth.”

With enough practice you will be able to round most numbers almost instantly. There is one case, however, that often leads to confusion. What happens if your rounding digit is a 9, and you need to round it up? The answer is that you round 9 up to 10 by writing 0 in the rounding place and adding 1 to the place to the left.

For example, suppose you want to round 429.5 to the nearest whole number (that is, to the ones place). Your rounding digit is 9, so you keep the 4 and 2. Because the next digit is 6, you round the 9 up to 10, writing 0 in the ones place and adding 1 to the 2 in the tens place. Then you zero out the 5. This gives you a rounded value of 430.0 or just 430.

How to Estimate

Now let’s consider estimation. We estimate the result of a messy calculation by substituting a simpler calculation that gives a useful approximate answer. We often estimate by rounding some of the numbers in the messy calculation.

For example, suppose you need to buy 12 copies of a book that costs $18.76, and you want to know about how much the total will be. The exact answer is 12×$18.76, but that is hard to do in your head. So, you might estimate the total by rounding 12 down to 10 and calculating 10×$18.76=$187.60. Or you might estimate by rounding $18.76 up to $20 and calculating 12×$20=$240. Or you might even round both numbers, calculating 10×$20=$200. These are all legitimate ways to estimate the total. They are also all reasonably close to the exact value of 12×$18.76=$225.12.

The takeaway is that there may be several good ways to estimate the result of a calculation. An estimate is good as long as it is accurate enough to be useful.

Here is an example for you to practice. You are a teacher with a $500 budget to buy scientific calculators for a class of 37 students. You are on the phone with a vendor who will sell you scientific calculators for $9.49 each. Can you purchase the calculators at this price and stay within your budget? You need to make a quick estimate in your head to see if it is worth asking the vendor for more details. Estimate the cost of buying 37 calculators at this price. Pause the video while you make your estimate, and then continue the video to see how your answer compares to mine.

This is another example in which there are several good ways to make the estimate. You can round the 37 students up to 40 and the $9.49 price down to $9 to get an estimate of 40×$9=$360. You can also leave the 37 unrounded and round the $9.49 price up to $10 to get an estimate of 37×$10=$370. Rounding $9.49 up to $10 is not standard rounding; but $10 is a very simple number to work with, and it is still close enough to give you a useful estimate. In fact, rounding the price up has an added benefit. By rounding up, you guarantee that your estimate is an overestimate—a total higher than the exact answer.

Since the overestimate still falls within your $500 budget, you can be certain that the exact price of the calculators will be under $500. You can even take this approach one step further by rounding the class size of 37 up to 40 in addition to rounding the price up to $10 to get an overestimate of 40×$10=$400, also within the $500 budget. Now you know that you can afford this vendor’s price, and it is reasonable to continue the phone call to find out other details.

Keep in mind that this list of estimates is not exhaustive. You might come up with an estimate that is different but still valid and useful. And we should note that all these estimates are reasonably close to the exact value of 37×$9.49=$351.13.

In this lesson we learned that rounding is a way of simplifying numbers and estimation is a way of simplifying calculations. We round a number when we are more interested in the “big story” than the details. We estimate the value of a calculation when the extra labor of getting an exact answer is unnecessary, impossible, or meaningless.

The rounding and estimation guidelines in this video are widely used and will serve you well under most circumstances. But be aware that some circumstances and some jobs and fields of study call for different rounding and estimation rules. If you ever work in one of those fields, be sure to learn and follow its rules.

I hope this video was helpful. Thanks for watching, and happy studying!

Frequently Asked Questions

Rounding Practice Problems