
Hey guys! Welcome to this video on finding the area and perimeter of a shape.
The area and perimeter help us to measure two-dimensional shapes.
The area measures the surface of a shape, and perimeter measures the distance around the outside of a shape.
We’ll take a look at how to calculate each, but let’s start with perimeter.
Calculating Perimeter
To calculate the perimeter of any polygon, you add up the length of all the sides. For reference, a polygon is any two-dimensional closed shape that’s composed of straight lines.
Perimeter of a Rectangle
Let’s use a rectangular swimming pool as an example.

We want to add a safety fence along the outside of the pool. In order to figure out how much material is needed, we first need to figure out the perimeter of the pool. The length of the pool is 15 ft, and the width is 7 ft.

Because it’s a rectangle, we know that the opposite sides are congruent to each other.
This is all the information we need. Let’s add up all of the sides!
Assuming 15 is equal to \(a\), and 7 is equal to \(b\), we can use the following formula: \(\text{Perimeter} = a + a + b + b\).
Now let’s plug in our numbers. \(P=15\text{ ft}+15\text{ ft}+7\text{ ft}+7\text{ ft}\). Added together, we get 44 feet.
Alternatively, since we know that there are four sides and that there are two sets of identical sides, we can simplify our formula to \(P=2a+2b\). Let’s give it a whirl—I bet we get the same result.
Perimeter of a Square
We can apply this same sort of principle to finding the perimeter of a square.
A square has four equal sides, so we can say that the perimeter of a square is \(4 \times a\).
This principle also applies with an equilateral triangle. Because all three sides are the same, \(P=3 \times a\). An isosceles triangle has two sides that are the same, so the perimeter is \(2a+b\). I think you get the point.
Now, the only shape whose perimeter may seem a little less obvious to find is our friend the circle. You may have heard of the term circumference. Circumference is the measurement of the distance around a circle, which is similar to the perimeter of a polygon.
Because there are no straight sides on a circle, the circumference can be calculated by multiplying the diameter of the circle times pi (\(C=\pi d\)) or by multiplying the radius times 2 times pi (\(C=2\pi r\)).
Okay, we’ve covered perimeter, now let’s move on to area.
How to Find Area
When we were looking at the perimeter of different shapes, we were able to simplify the formulas. This gave us different formulas for different shapes, but each one followed the same principles.
Similarly, when finding the area of an object, the formula will be different for different shapes, but they all serve the same purpose: calculating the amount of space a shape occupies.
So, let’s take a look at different shapes and their area formulas.
Area Formulas
A square, a rectangle, and a parallelogram all share a formula, which is \(A=bh\), commonly referred to as “length times width.”
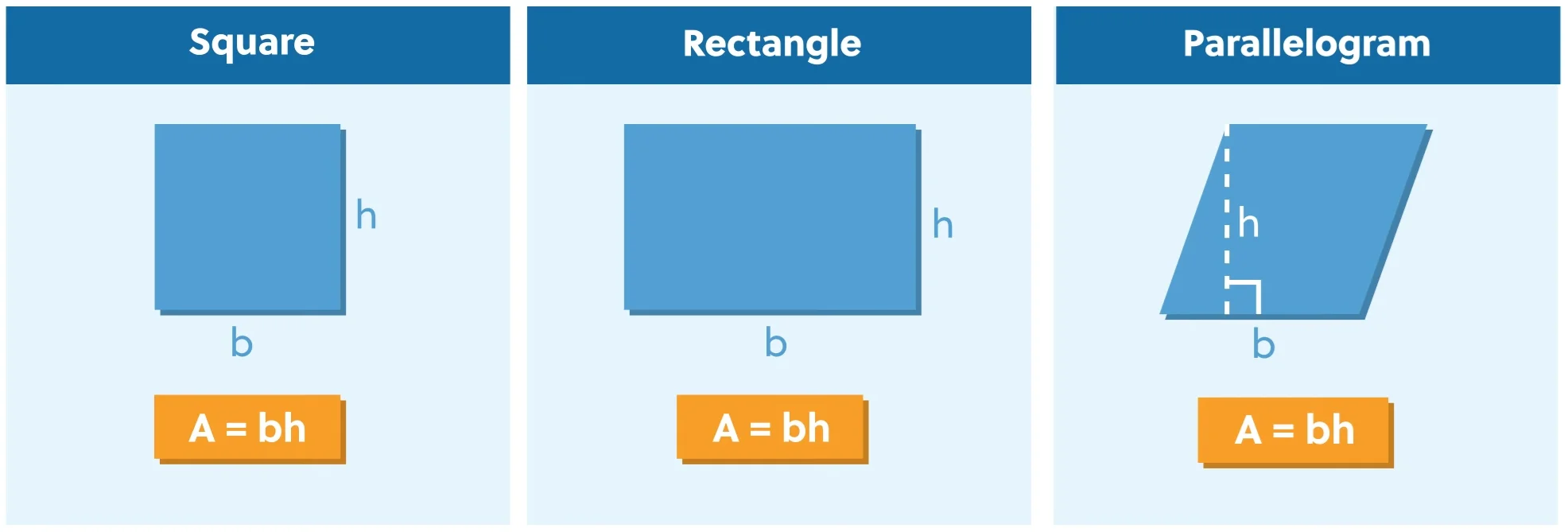
The area of a triangle is \(A=\frac{1}{2}bh\).
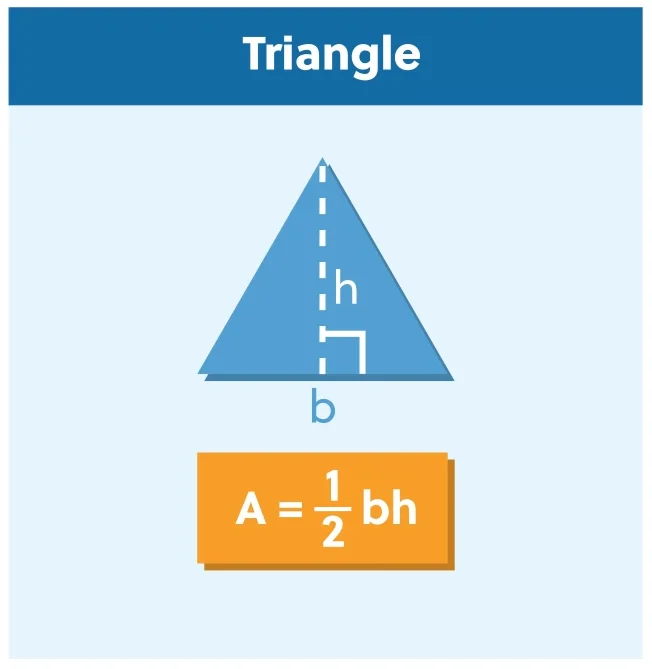
The area for a trapezoid is \(A=\frac{1}{2}(b_1+b_2)h\).
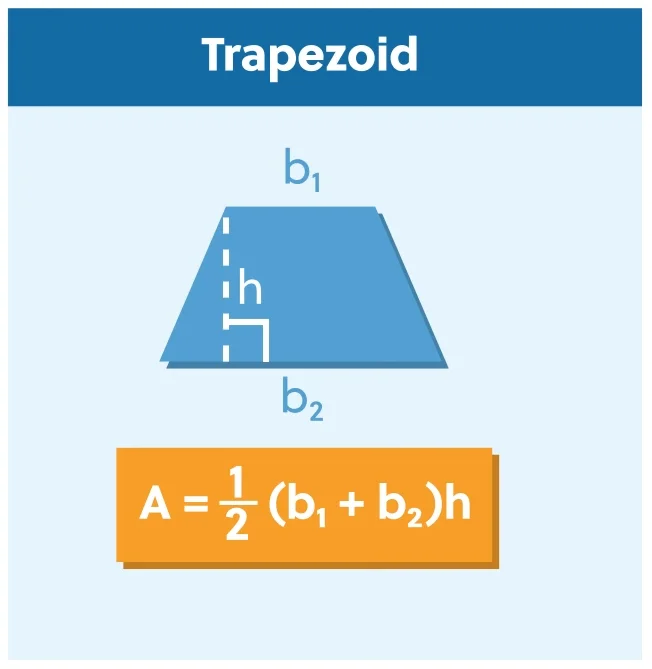
The area of a circle is \(A=\pi r^2\).
Now let’s look at some examples of how to solve for the area of a triangle and the area of a trapezoid.
Area of a Triangle Example
Given that a triangle has a base of 6 centimeters and a height of 4 centimeters, calculate the area by substituting the values into the triangle area formula (\(A=\frac{1}{2}bh\)). It’s important to know that the height of a triangle will always make a right angle with the base.
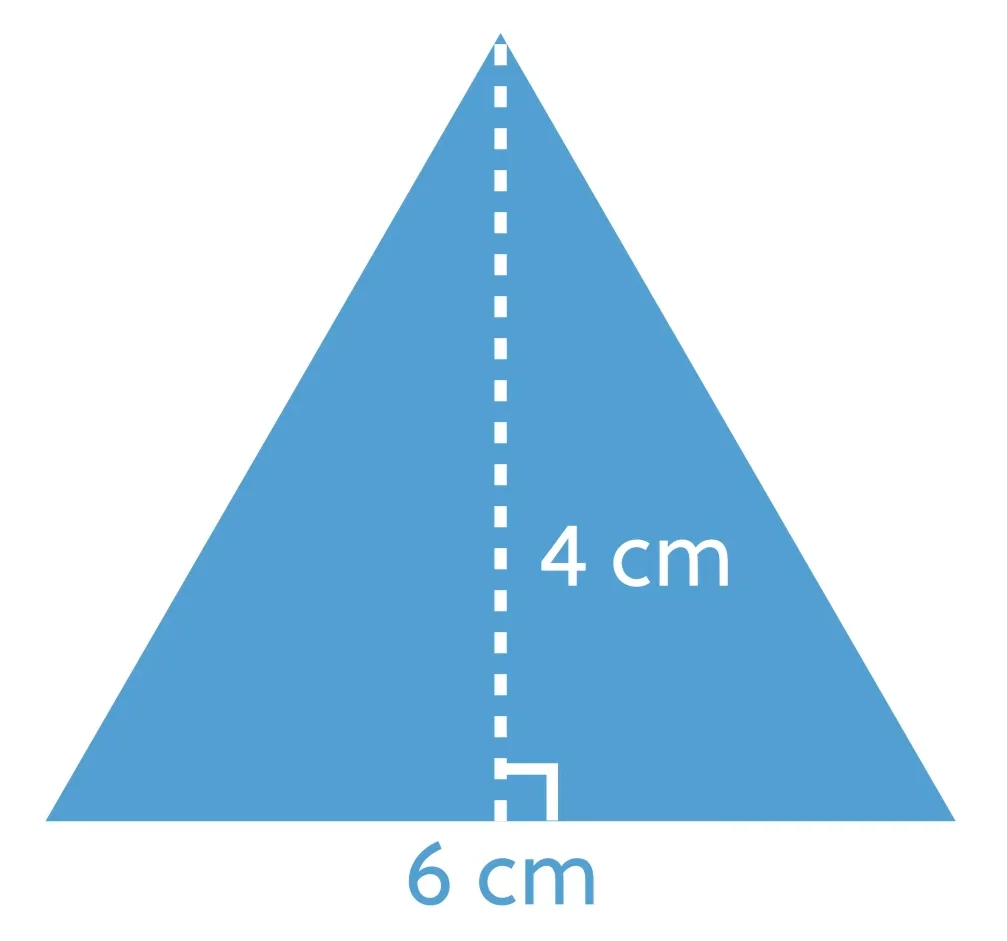
Start by multiplying 6 times 4 to get a product of 24.
Then, multiply 1/2 times 24 (the same as dividing by 2), which gives us a solution of 12 cm2.
Area of a Trapezoid Example
Now, let’s say you have a trapezoid with a height equal to 7 inches, base 1 equal to 8 inches, and base 2 equal to 6 inches.
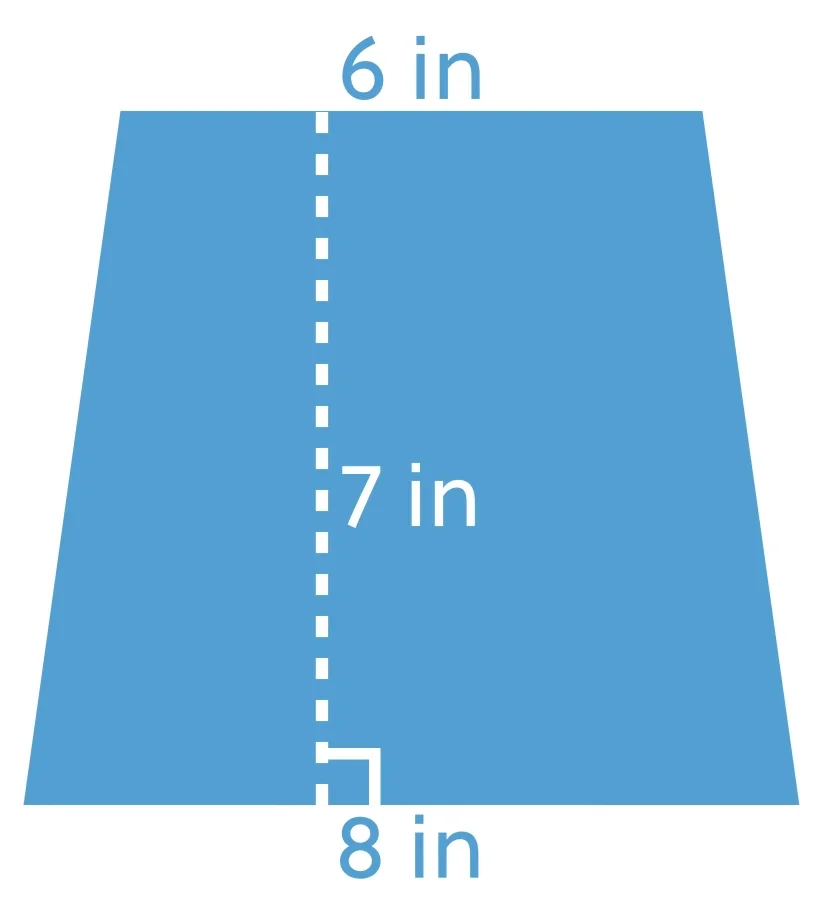
Given this, we can substitute our numbers into the formula for the area of a trapezoid:
Start by finding the sum of 8 and 6.
Then, multiply 14 by 7 to get a product of 98.
Finally, you can multiply 98 by 1/2 or divide 98 by 2 to get a solution of 42 in2.
That’s it for this review. Thanks for watching, and happy studying!
Frequently Asked Questions
Q
How do you find area?
A
Each shape has a unique area formula. Here are some of the most common:
Circle: \(A=πr^2\)
Square: \(A=s^2\)
Rectangle: \(A=lw\)
Triangle: \(A=\frac{1}{2}bh\)
Parallelogram: \(A=bh\)
Trapezoid: \(A=1/2 (b_1+b_2)h\)
Q
How do you find the perimeter?
A
Find perimeter by adding together the lengths of each side of the figure.
Ex. What is the perimeter of this figure?
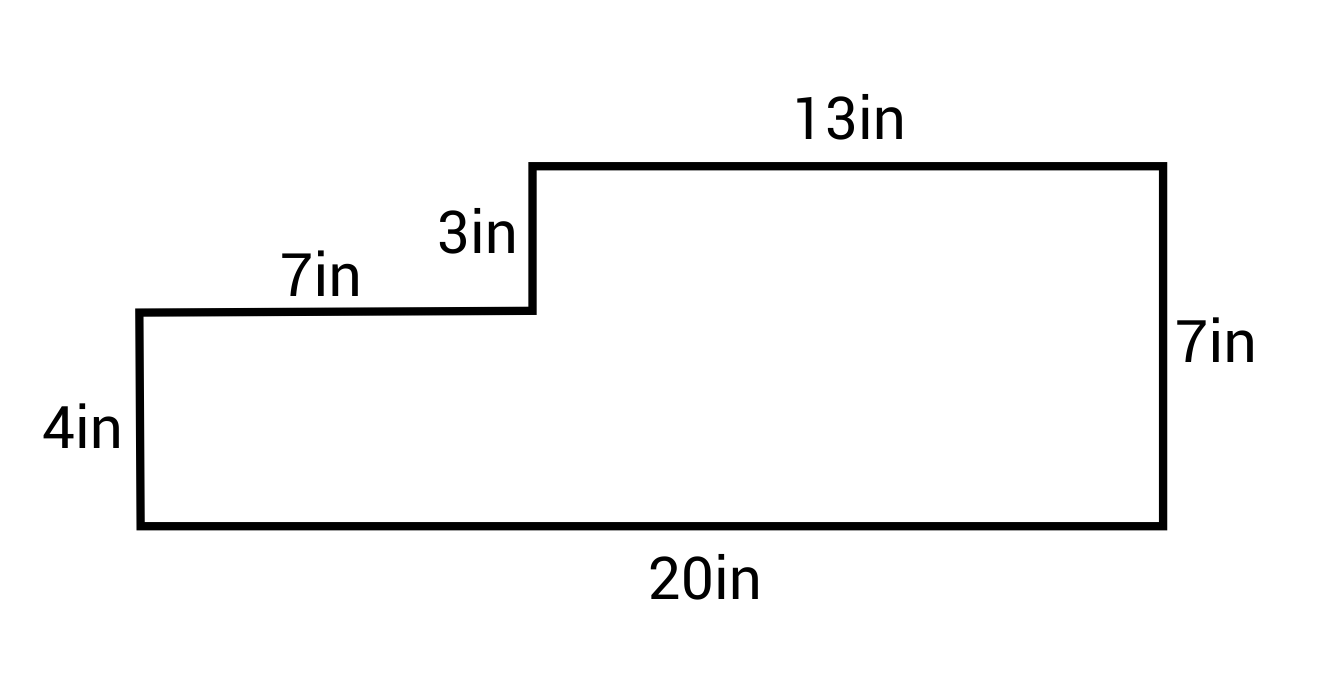
P = 4 + 7 + 3 + 13 + 7 + 20 = 54 in
Q
How do you find the area of a triangle?
A
The most common way to find the area of a triangle is by multiplying its base times its height and dividing by 2.
\(A=\frac{1}{2}bh\)
Some other triangle area formulas are:
Any triangle: \(A=\sqrt{s(s-a)(s-b)(s-c)}\), where s is the semi-perimeter (half the perimeter), and a, b, and c are side lengths.
Isosceles triangle: \(A=\frac{1}{2}b \sqrt{(a^2-\frac{b^2}{4})}\), where b is the unique side and a is the length of one of the two congruent sides.
Equilateral triangle: \(A=\frac{\sqrt{3}}{4}a^2\), where a is the length of a side.
Ex. What is the area of this triangle?
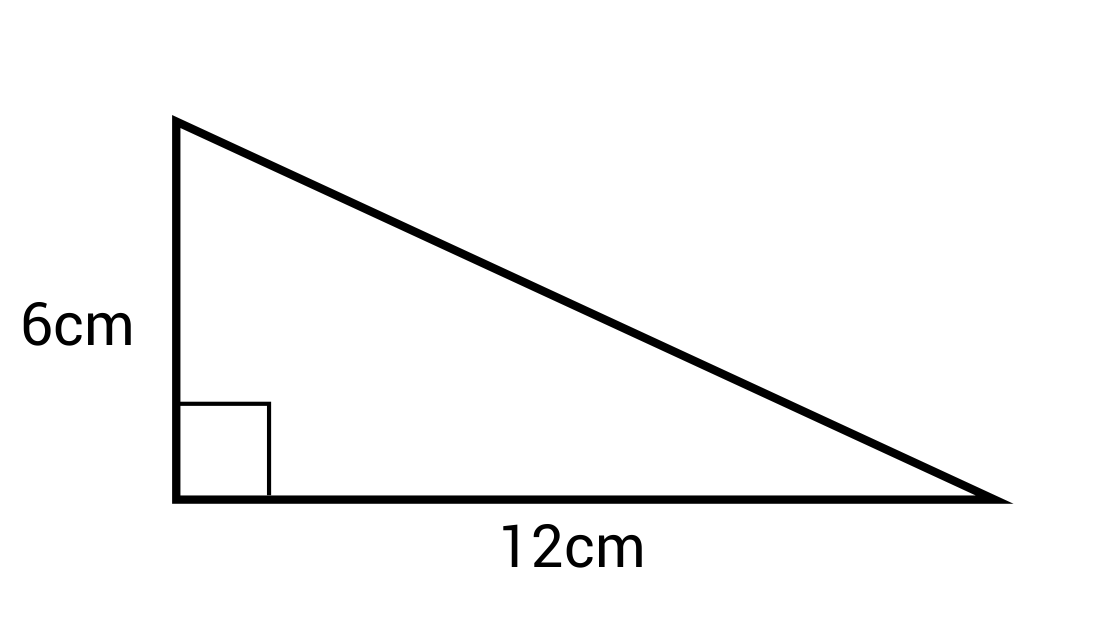
\(A=\frac{1}{2} bh=\frac{1}{2} (12)(6)=36 cm^2\)
Q
How do you find the perimeter of a rectangle?
A
Find the perimeter of a rectangle by multiplying its length by 2 and its width by 2 and adding the values, or by adding its length and width and then multiplying by 2.
P = 2l + 2w or P = 2(l + w)
Ex. What is the perimeter of this rectangle?
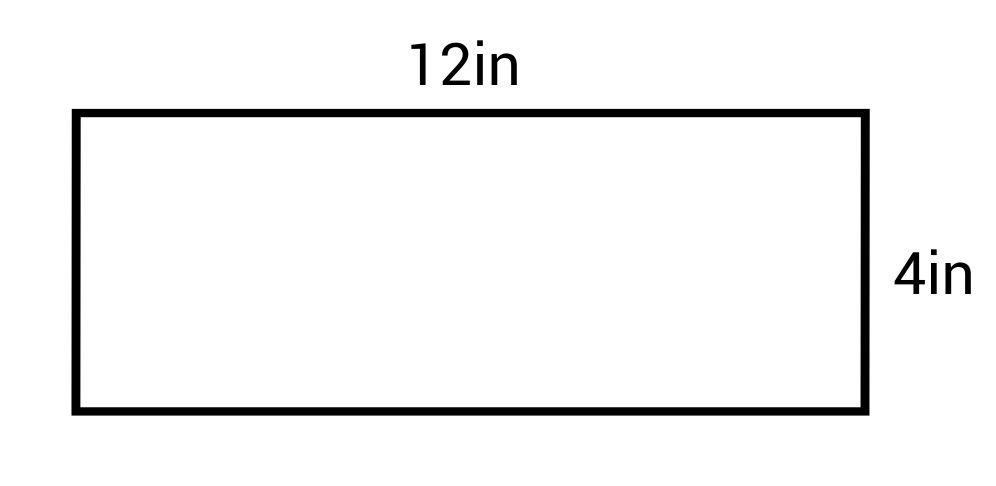
P = 2(12) + 2(4) = 24 + 8 = 32 in or P = 2(12 + 4) = 2(16) = 32 in
Q
How do you find the area of a circle?
A
Find the area of a circle by multiplying pi (π) times the radius squared.
\(A=πr^2\)
Ex. What is the area of this circle?
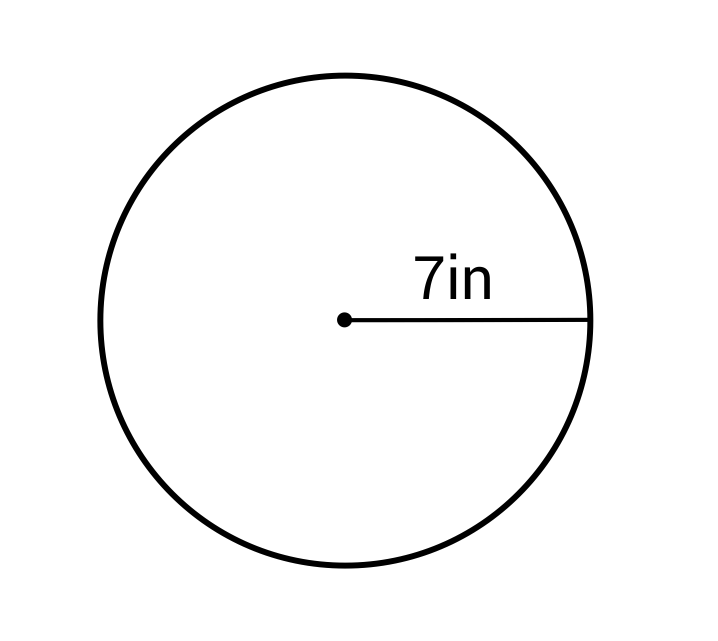
\(A=π(7)^2=49πin^2≈156.86in^2\)
Q
How do you find the perimeter of a triangle?
A
Find the perimeter of a triangle by adding the lengths of all three sides together.
Area and Perimeter Practice Problems
What is the area of this rectangle?
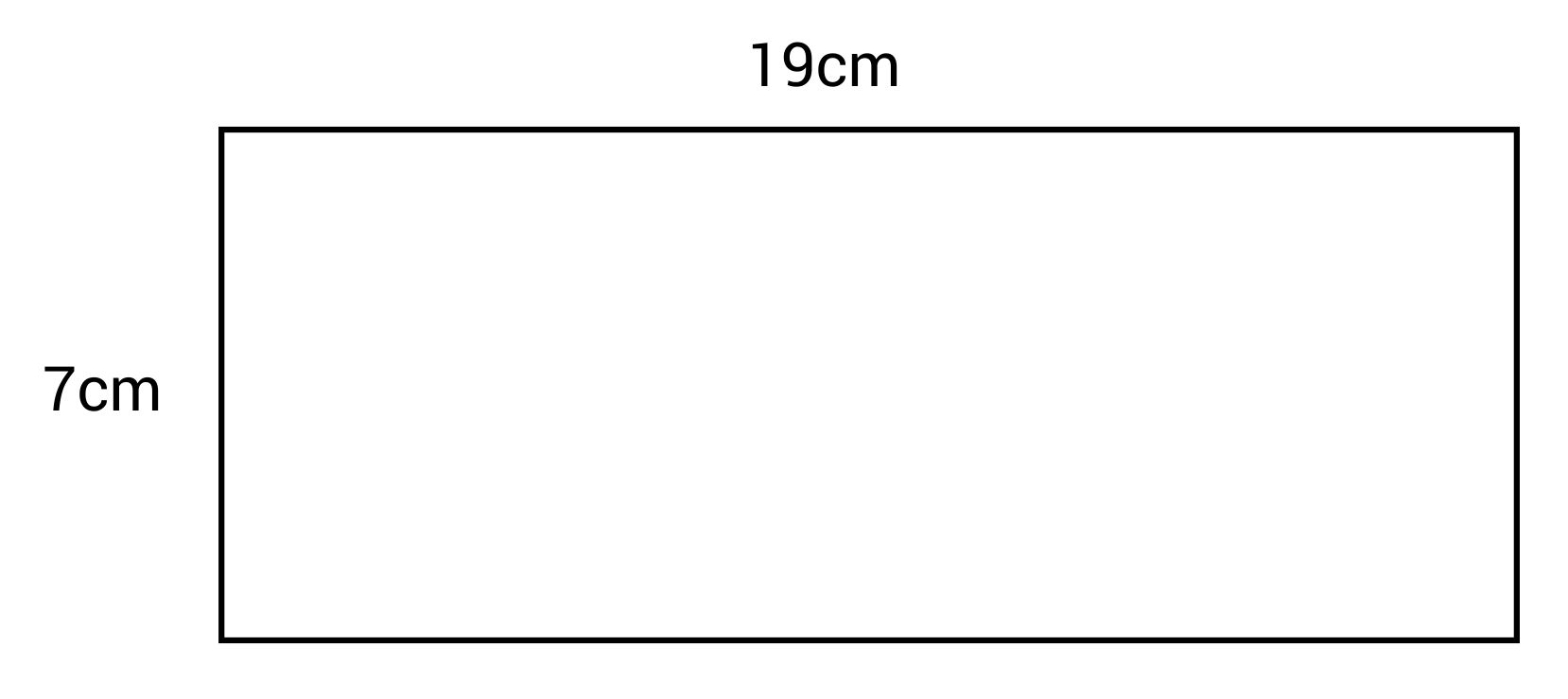
The correct answer is 133 cm
\(A=lw\)
The length is 19 cm and the width is 7 cm.
\(A=19\times7=133\text{ cm}^2\)
What is the area of a square with a side length of 4 in?
The correct answer is 16 in2. To find the area of a square, square the length of its side.
\(A=s^2\)
\(A=(4)^2=16\text{ in}^2\)
What is the perimeter of this rectangle?
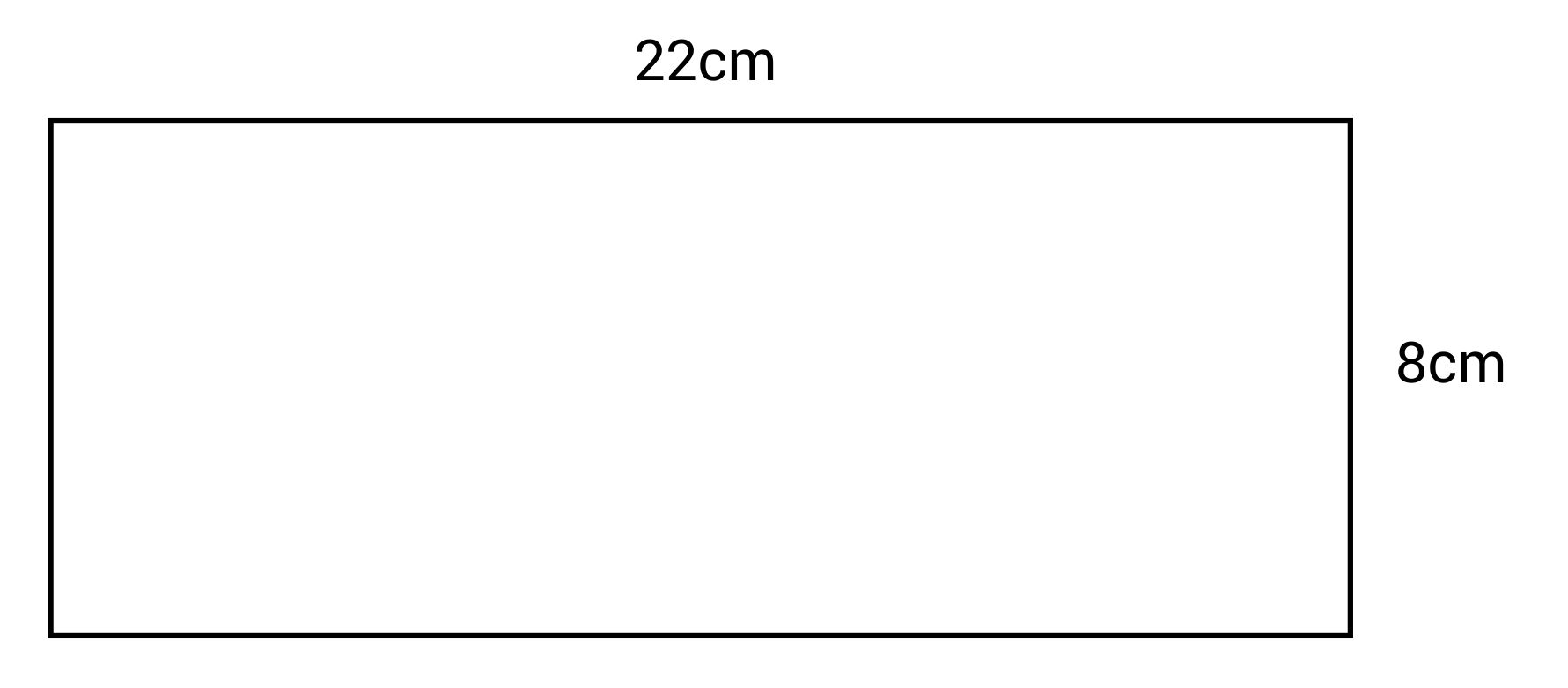
The correct answer is 60 cm. The formula for perimeter of a rectangle is:
\(P=2(l+w)\) or
\(P=2l+2w\)
The length is 22 cm and the width is 8cm.
\(P=2(22+8)=2(30)=60\text{ cm}\)
What is the perimeter of this pentagon?

The correct answer is 38 ft. Find the perimeter of a figure by adding the lengths of all the sides together.
\(P=9+9+7+6+7=38\text{ ft}\)
What is the formula for finding the perimeter of a rectangle?
The correct answer is \(P=2l+2w\). Find the perimeter of a rectangle by adding double the length plus double the width, or add the length and width together and then double that number.