Calculating Areas Using Integration

When it comes to finding the areas of different shapes, geometry formulas help us out a lot. However, they have their limitations. For example, if we wanted to find the area of an irregular shape like this, there aren’t any quick and handy formulas for that.

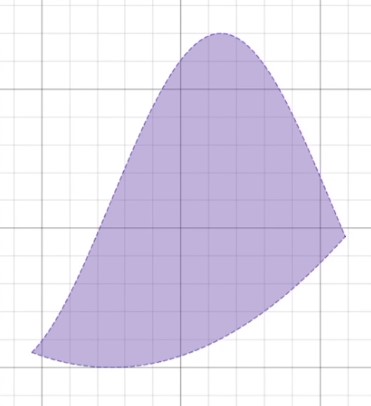
Recall that we previously used Riemann sums as a technique for handling the similar problem of finding the area beneath a curve. In this video, we are going to discuss how to use integrals as a faster, more accurate method of finding such areas, and how to handle more irregular shapes with integrals.

Given a function, we can determine its slope at any given point by taking the derivative of the function. But what information do we gain by doing the opposite, taking the integral of the function? The integral of a function tells us about the area beneath the curve. This means that instead of worrying about time-consuming Riemann sums with margins of error, we can get the exact area underneath a curve by taking the definite integral of the function over the domain of interest.

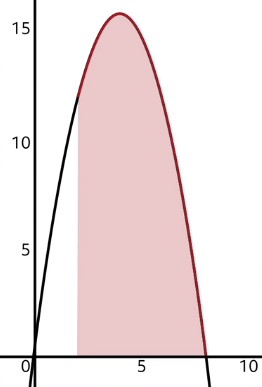
For example, if we wanted to find the area underneath the function \(f(x)=-x^{2}+8x\) from \(x=2\) to \(x=8\), we would need to take the definite integral of \(f\) and evaluate with upper bound at 8 and lower bound at 2:

To solve this integral, we can integrate each term separately.

 
Now we just need to evaluate this integral from 2 to 8. To evaluate, we first need to plug in the larger number, 8, anywhere we see an \(x\), and then we’ll subtract the function when we plug in 2 anywhere we see an \(x\).

Now we can simplify a little bit.

So the area under the curve from \(x=2\) to \(x=8\) is equal to 72.

Earlier when I said that the integral tells us the area beneath a curve, that was a bit of a condensed explanation. Technically the integral of a function tells us how much area is beneath the curve to the left of whatever point \(x\) we plug in. So when we plugged in 8 into the integrated function, we determined that the area beneath the curve to the left of 8 is equal to \(\frac{256}{3}\). Now, since we were not interested in all of the area to the left of 8, only the area between \(x=8\) and \(x=2\), we had to eliminate all of the area to the left of 2. This is why we subtracted the area we got by plugging in 2, which was \(\frac{40}{3}\).

Sometimes, we may be interested in more complex shapes, such as the one pictured in the beginning of this video. This shape actually happens to be the area between two functions.

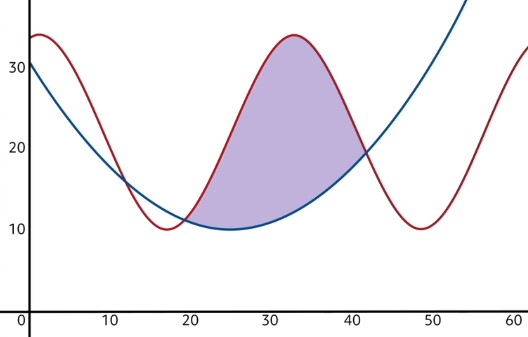
In order to find the area of such a region, we need to use a similar subtraction trick to what I just described. In problems where the area between two curves must be found, we first have to determine which of the two functions is “on top”. In this case, the red oscillating function is the one on top, and the blue parabola is the bottom function over the domain of interest. Our next step is to use a definite integral to find the area beneath the top function.

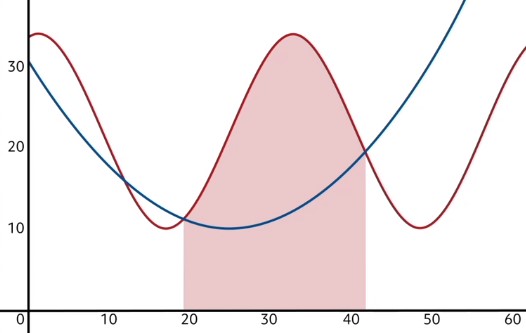
Since this clearly counts for too much area, we need to take away some of it. Specifically, we need to eliminate the area below the bottom function. In other words, we will find the area beneath the blue curve in that same domain, and subtract it from the red area. This will leave us with only the area between the curves!

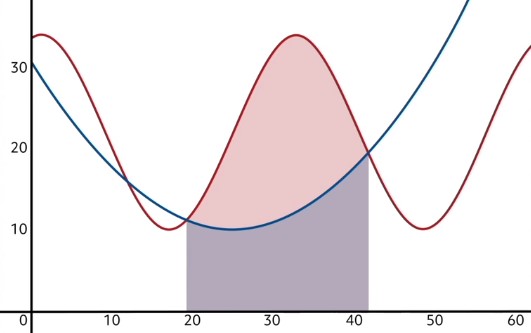
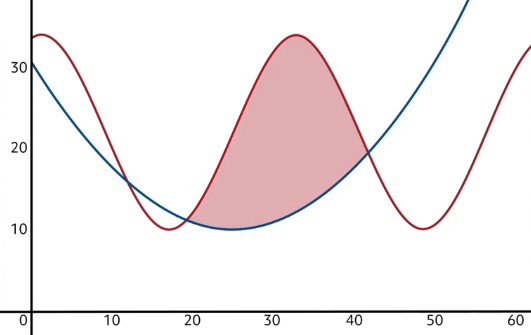
Let’s apply this concept now.

A sculptor is cutting pieces of aluminum for a new artwork to be installed near city hall. One of the pieces is shaped such that one of its edges is defined by the curve \(f(x)=x^{2}\) on the domain \(x=[0,1]\), and the other edge is defined by the curve \(g(x)=\sqrt{x}\) on the same domain. Find the area (in square meters) of this aluminum piece by getting the area between the curves \(f(x) \)and \(g(x)\) on the domain \(x=[0,1]\).

The first step in this type of problem is always checking to see which function is on top. One helpful method for doing so is graphing the two functions.

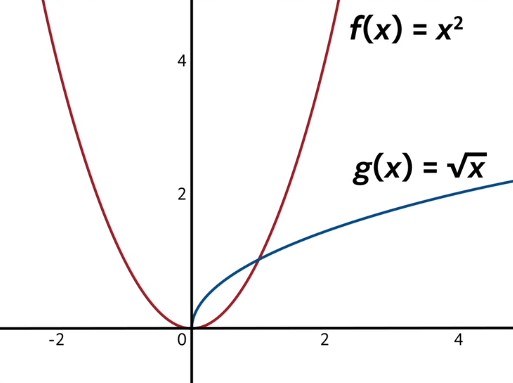
Since we are considering the domain from \(x=0\) to \(x=1\), we can see that our top function is \(g(x)=\sqrt{x}\), while the bottom function is \(f(x)=x^{2}\). Let’s now find the area under the upper function by integrating \(g(x)\) from 0 to 1.

We can rewrite the square root of \(x\) as \(x\frac{1}{2}\) to make it easier to integrate.

Now, we add one to the exponent, and then divide by the new power.

Now we can evaluate.

Evaluating our function at 0 being equal to 0 makes sense because the square root function is undefined to the left of the origin, and with no curve, there would be no area beneath! So the area under \(g(x)\) from 0 to 1 is equal to \(\frac{2}{3}\).

Now, we need to eliminate from this area what lies beneath \(f(x)\). Let’s calculate that area now.

Again, we’re going to evaluate by plugging in 1 and 0.

So the area beneath our function \(f(x)\) on the interval from 0 to 1 is \(\frac{1}{3}\).

The area between \(g(x)\) and \(f(x)\) on the domain \(x=0\) to \(x=1\) is then equal to:

So the sculptor will use \(\frac{1}{3}\) square meter of aluminum for this piece of the sculpture.

Not so bad right? I do want to point something out though. Sometimes, when a problem asks for the area between two curves, the functions will actually cross over each other within the domain of interest. For example, if in the previous problem we wanted to know about the area between \(g(x)\) and \(f(x)\) on the domain \(x=0\) to \(x=2\), we would then be considering this area, which consists of two pieces:

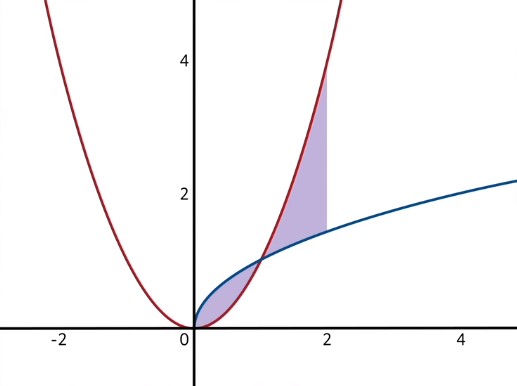
In this case, after the point \(x=1\), the functions swap places so that \(f(x)=x^{2}\) is now on top, and \(g(x)\) is on the bottom. To handle this issue, we have to break the area up into sections and integrate those sections separately. The first section would be from \(x=0\) to \(x=1\) (and we would solve for the area exactly as we just did). The second section would be from \(x=1\) to \(x=2\), where the functions swap places. The area of the second section can be found much like the area of the first, but of course because of the swap, you must first find the area under \(f(x)\) and then subtract the area beneath \(g(x)\).

Now let’s take a look at another area enclosed by two functions.

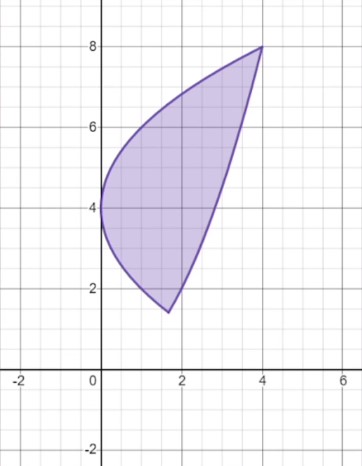
Something is different about this shape. In previous examples, the areas have each had distinct upper and lower edges, whereas this one seems to have a left and a right edge. Remember the vertical line test from algebra? It states that if at any point a curve on the plane has one point above another vertically, that curve is not a function of \(x\). In this case, we can see that the left edge of this shape fails the vertical line test and is therefore not a function of \(x\). Can we still find the area between these curves using integrals?

We will have to change our approach slightly, but yes we can! Whenever one or both of the curves fail the vertical line test, we must take their integrals with respect to \(y\). And while this may seem daunting, these kinds of problems will usually either give the equations of the curves already in the form “\(x\) in terms of \(y\)”, or you will easily be able to rearrange them into this format.

Let’s quickly look at some shapes and determine whether we would integrate with the respect to \(x\) or \(y\) to find their area.

For this shape, notice that it has distinct upper and lower edges. Do both of these edges pass the vertical line test individually? Yes, they do! Because they both qualify as functions of \(x\), we can find this area by integrating with the respect to \(x\), as usual.

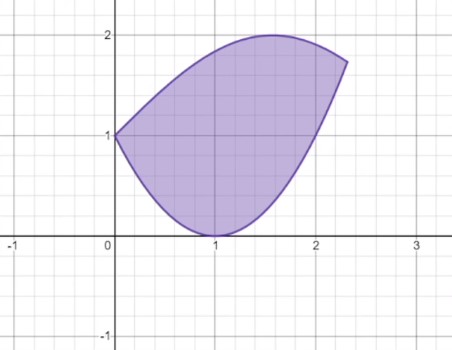
What about this shape? Instead of a clear upper and lower edge, this shape has a left and right edge, both of which fail the vertical line test. Remember, if one or both edges fail the vertical line test, then the area must be found by integrating with the respect to \(y\) instead of \(x\), so that’s how this problem would be solved.

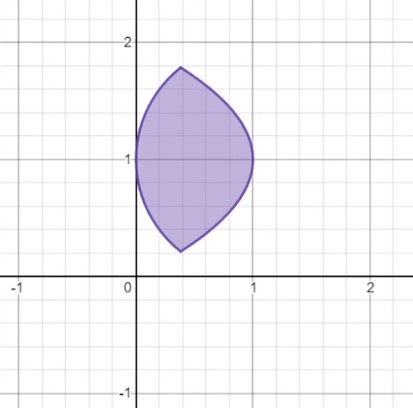
Let’s try one more. This shape is a bit of a special case, so let’s think through it carefully. Like the previous one, it seems to have a left and right edge… but in a way it also seems to have an upper and lower edge doesn’t it? There are actually two ways of looking at this particular shape, since it has one side that is perfectly horizontal and one that is perfectly vertical. If we consider the left and right walls as edges, we must integrate with the respect to \(y\) because the left wall is a vertical line and therefore fails the vertical line test. In this case, the bounds of integration would be from \(y=0\) to \(y=2\). If, however, we consider the flat top and the parabola below it to be the two edges, then both of these pass the vertical line test and we may integrate with respect to \(x\). From this perspective, the bounds of integration would be from \(x=0\) to \(x=1\). You likely won’t run into many problems that look like this, but if they do come your way, carefully consider which edges do or do not pass the vertical line test before proceeding.

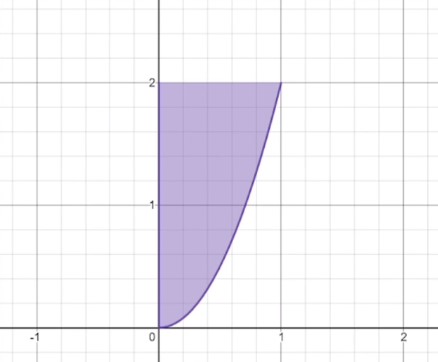
Let’s try one more problem; this time, a full example of integrating with the respect to \(y\). Find the area of the shaded region beneath the curves \(y=x^{2}\) and \(x=\frac{1}{4}y^{2}-\frac{3}{2}y+\frac{9}{4}\).

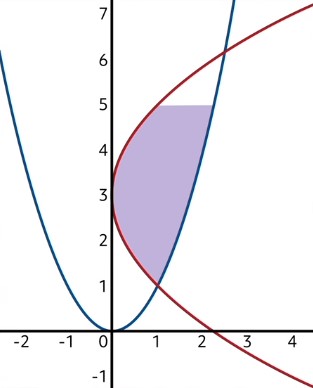
Notice again that one of the curves fails the vertical line test, confirming that we must integrate with the respect to \(y\). Also, notice that the shaded region stops at the height \(y=5\). We will need to reflect this cutoff in the bounds of the definite integrals by making 5 the upper bound.

Now, usually in these area problems we need to find out which function is on top and which is on bottom. But since we must work this problem in terms of \(y\), we instead need to find out which function is farther right, and treat that one as the top function (since farther right implies a greater \(x\)-value). In this case, \(y=x^{2}\) is the rightmost function, while \(x=\frac{1}{4}y^{2}-\frac{3}{2}y+\frac{9}{4}\) is the left one.

Let’s go ahead and solve the right function’s integral. Of course, we first need to rearrange \(y=x^{2}\) to have \(x\) by itself on one side. Taking the square root of both sides, we get that \(x=\sqrt{y}\). Now we can integrate, and remember, our bounds of integration will be from \(y=1\), since that’s the lowest point of the shaded region, to \(y=5\), the highest point of the shaded region.

So the area to the left of \(x=\sqrt{y}\) from \(y=1\) to \(y=5\) is about 6.78.

Now, we must get rid of the area to the left of the other function. Let’s set up that integral now.

This integral is fairly straightforward, as long as we take it one term at a time:

So if we plug in 5 for all of our \(y\)-values and then subtract plugging in 1 for all of our \(y\)-values, we’ll get this:

Putting it all together, the area of the shaded region is then equal to \(6.78-1.34=5.44\)

As we’ve seen in this lesson, with the help of definite integrals, we can find the areas of countless irregular shapes, as long as their edges can be described as functions. Whenever you need to find the area between two functions, first find the area beneath the upper function, then subtract the area beneath the lower function. In some cases, the two functions will cross paths and swap places as top and bottom. Whenever this happens, you can still find the area between them, but with an added step. You must chop the domain into sections and handle each separately. Finally, you can even find areas between curves that do not qualify as functions of \(x\); if they can be written as functions of \(y\), you can solve their integrals with the respect to \(y\).

Because we’ve covered so much ground in this lesson, you might find it helpful to watch through the video again. But with a little repetition and practice, you’ll have the hang of it and be ready to tackle any of these types of problems!

Thanks for watching, and happy studying!